
����Ŀ������������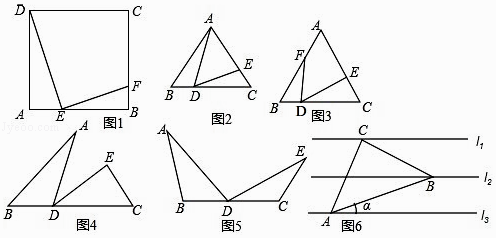
��1����ͼ1����֪E�Ǿ���ABCD�ı�AB��һ�㣬EF��DE��BC�ڵ�F��֤������ADE�ס�BFE��
��2��������ƵĻ���ͼ������ĸK�����Գ�Ϊ��K�������ƣ�������Ϊͼ�εĽṹ������һ��������3����ֱ��ϵ��Ҳ������Ϊ��һ������ֱ��������ͨ��3���Ƚ��ֻ������أ�
��ʽһ��ͼ2����֪�ȱ�������ABC����D��E�ֱ�ΪBC��AC�ϵĵ㣬��ADE=60�㣮
��ͼ������������������˵�����ɣ�
����ͼ3��������ADE�ڡ�ABC���ڲ�����ADE���߲���BC�غϣ����Ƶ�D��ʱ����תһ���ĽǶȣ�����������������
��3����ʽ����ͼ4�����ر�ʽ1ͼ���е��߶�AE���ڵõ�����ͼ���У�
�������B=��C=��ADE=50�㣬ͼ������������������˵�����ɣ�
����ͼ5������B=��C=��ADE=��a����aΪ����ǣ�����������������
��4����ʽ����֪����������ƽ��ֱ��ľ�����ȣ�������ֱ�ǡ�ABC����������ֱ���������ƽ��ֱ���ϣ���cosa��ֵ����ֱ��д���������
���𰸡�
��1��
�⣺���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬
���ADE+��AED=90�㣬
��EF��DE��
���AED+��BEF=90�㣬
���ADE=��BEF��
�ߡ�A=��B=90�㣬
���ADE�ס�BEF
��2��
�⣺�١ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
���������ε��ڽǺͶ����ã���ADB+��BAD=120�㣬
�ߡ�ADE=60�㣬
���ADB+��EDC=120�㣬
���BAD=��CDE��
�ߡ�B=��C=60�㣬
���ABD�ס�CDE
�ڡߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
���������ε��ڽǺͶ����ã���FDB+��BFD=120�㣬
�ߡ�FDE=60�㣬
���FDB+��EDC=120�㣬
���BFD=��CDE��
�ߡ�B=��C=60�㣬
���FBD�ס�CDE��
��3��
�⣺�١�B=��C=50�㣬
���������ε��ڽǺͶ����ã���ADB+��BAD=130�㣬
�ߡ�ADE=50�㣬
���ADB+��EDC=130�㣬
���BAD=��CDE��
�ߡ�B=��C=130�㣬
���ABD�ס�CDE
��B=��C=�������������ε��ڽǺͶ����ã���ADB+��BAD=180�㩁����
�ߡ�ADE=����
���ADB+��EDC=180�㩁����
���BAD=��CDE��
�ߡ�B=��C=����
���ABD�ס�DCE��
��4��![]()
���������⣺��4������A��A��l1 �� ����B��BE��l1��l3��F��
���AFB=90�㣬
���CAD+��ACD=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬
���CAD=��BCE��
�ڡ�ACD�͡�BCE�У� 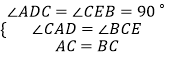 ��
��
���ACD�ա�BCE��
��AD=CE��CD=BE��
��ƽ����ľ���Ϊd��
��AD=CE=2d��BE=CD=d��
��DE=CD+CE=3d��
���ı���ADEF�Ǿ��Σ�
��AF=DE=3d��BF=d��
��Rt��ABF��AB= ![]() =
= ![]() d��
d��
��cos��= ![]() =
= ![]() =
= ![]() ��
��
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��x2y��3xy2+2x2y��y2x ����2��2��2a2��9b����3��3a2��7b����
��3��2a2��[![]() ��ab��4a2��+8ab]��
��ab��4a2��+8ab]��![]() ab.
ab.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�D��BC���е㣬��D���ֱ��GF��AC��F����AC��ƽ����BG��G�㣬DE��DF����AB�ڵ�E������EG��EF��

��1����֤��BG��CF��
��2�������ж�BE+CF��EF�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ��ǿ��̬���н��裬��̨�д�����չ��ɫ��ͨ��������������ɫ��ͨ��ϵ��2016��11��28�չ������г�½�������ڳ��У�������������������������ù������г����ﳵʱ�䣺����λ��h��������õ����ݷֳ����飬����������ͳ��ͼ�������ͼ����Ϣ������������⣮ 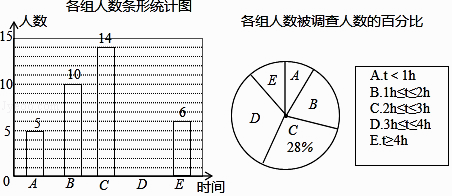
��1����α�������������Ƕ��٣�
��2�������ʾD�������Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
��3���������г�ϵͳͶ��ʹ�ú��涨����賵1Сʱ����ѣ�1Сʱ��2Сʱ�շ�1Ԫ��2Сʱ��3Сʱ�շ�3Ԫ��3Сʱ���ϣ���3Ԫ�Ļ����ϣ�ÿСʱ����3Ԫ������1Сʱ����1Сʱ���㣩����㣬�����ù������г��������У��ɷѳ���3Ԫ��������ռ�İٷֱȣ�
��4��A��5����3Ů2�У����������ȡ2�ˣ���ǡ����һ��һŮ��Ϊ�¼�A�����б���������״ͼ������¼�A�ĸ���P��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�����������y= ![]() x��ͼ����A����A��������Ϊ6������������y=
x��ͼ����A����A��������Ϊ6������������y= ![]() ��ͼ��Ҳ������A����һ�����ڵĵ�B�����������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB����
��ͼ��Ҳ������A����һ�����ڵĵ�B�����������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB���� 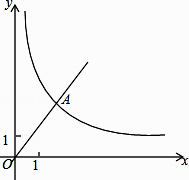
��1����������������Ľ���ʽ��
��2��ֱ��AB��һ�κ������ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˲μ�ѧУ��֯������ʵ��������ԣ����ڵ�5�β��Գɼ���ͼ��ʾ��

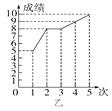
(1)�������ͼ�е�������д����
���� | ƽ���� | ���� | ���� |
�� | 8 | ||
�� | 8 | 2.8 |
(2)��ƽ�����ͷ������Ͽ���˭�ijɼ���Щ���ӷ�չ����������˭�ijɼ���Щ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������*������һ�������㣺��������������a��b���涨a*b=ab2+2ab+a��
�磺1*3=1��32+2��1��3+1=16
��1����2*����2����ֵ��
��2����2*x=m,![]() ������xΪ�����������ԱȽ�m��n�Ĵ�С��
������xΪ�����������ԱȽ�m��n�Ĵ�С��
��3����[![]() ]
]![]() =a+4����a��ֵ��
=a+4����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��5��5�����У�С����ı߳�Ϊ1.
(1)ͼ�и��������ABCD�����Ϊ________��
(2)������AC������ACΪ�ߵ������ε����Ϊ________��
(3)�����������л�һ����������Σ�ʹ����߶����ڸ������������������������������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ѵȱ���ABC����DE�۵�,ʹ��Aǡ������BC���ϵĵ�P��,��DP��BC,��BP=4cm,��AD�ij�Ϊ�� ��
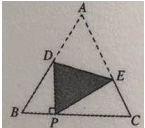
A. 5 B. 3 C. 4![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com