
【题目】用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)求2*(﹣2)的值;
(2)若2*x=m,![]() (其中x为有理数),试比较m,n的大小;
(其中x为有理数),试比较m,n的大小;
(3)若[![]() ]
]![]() =a+4,求a的值.
=a+4,求a的值.
【答案】(1)2;(2)m>n;(3)a的值为﹣![]() .
.
【解析】
(1)根据给定定义式,代入数据求值即可;
(2)根据给定定义式,表示出m和n,做差后即可得出结论;
(3)重复套用定义式,得出关于a的一元一次方程,解方程求出a值即可.
(1)2*(﹣2)=2×(﹣2)2+2×2×(﹣2)+2=2.
(2)m=2*x=2x2+2×2x+2=2x2+4x+2,n=(![]() x)*3=(
x)*3=(![]() x)×32+2×(
x)×32+2×(![]() x)×3+
x)×3+![]() x=4x,
x=4x,
m﹣n=2x2+4x+2﹣4x=2x2+2≥2,
故m>n.
(3)(![]() )*(﹣3)=
)*(﹣3)=![]() ×(﹣3)2+2×
×(﹣3)2+2×![]() ×(﹣3)+
×(﹣3)+![]() =2a+2,(2a+2)*
=2a+2,(2a+2)*![]() =(2a+2)×(
=(2a+2)×(![]() )2+2×(2a+2)×
)2+2×(2a+2)×![]() +(2a+2)=
+(2a+2)=![]() +
+![]() ,
,
即a+4=![]() +
+![]() ,解得:a=﹣
,解得:a=﹣![]() .
.
答:当[![]() ]
]![]() =a+4时,a的值为﹣
=a+4时,a的值为﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )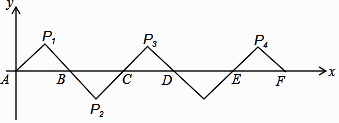
A.(4030,1)
B.(4029,﹣1)
C.(4033,1)
D.(4031,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和为 . 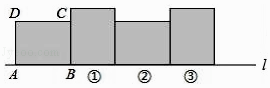
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答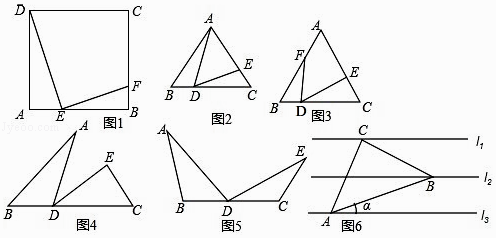
(1)如图1,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,证明:△ADE∽△BFE.
(2)这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”,那普通的3个等角又会怎样呢?
变式一如图2,已知等边三角形ABC,点D、E分别为BC,AC上的点,∠ADE=60°.
①图中有相似三角形吗?请说明理由.
②如图3,若将∠ADE在△ABC的内部(∠ADE两边不与BC重合),绕点D逆时针旋转一定的角度,还有相似三角形吗?
(3)变式二如图4,隐藏变式1图形中的线段AE,在得到的新图形中.
①如果∠B=∠C=∠ADE=50°,图中有相似三角形吗?请说明理由.
②如图5,若∠B=∠C=∠ADE=∠a,∠a为任意角,还有相似三角形吗?
(4)交式三已知,相邻两条平形直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则cosa的值是(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
(1)a= ,b= .
(2)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是王老师在数学课堂上给同学们出的一道数学题,要求对以下实数进行分类填空:
-![]() ,0,
,0,![]() ,
,![]() ,18,
,18,![]() ,
,![]() ,-0.56,3.14159,
,-0.56,3.14159,![]() ,
,![]() ,
,![]() ,0.8080080008…,-
,0.8080080008…,-![]() .
.
(1)有理数集合:________________________________________________________________________;
(2)无理数集合:________________________________________________________________________;
(3)非负整数集合:________________________________________________________________________;
(4)分数集合:________________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考: 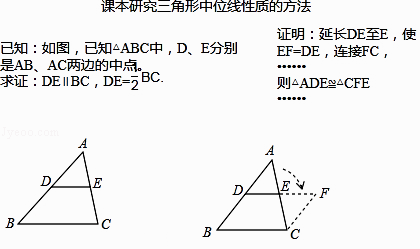 请你利用小亮的发现解决下列问题:
请你利用小亮的发现解决下列问题:
(1)如图1,AD是△ABC的中线,BE交AC于E,交AD于E,且AE=EF,求证:AC=BF. 请你帮助小亮写出辅助线作法并完成论证过程: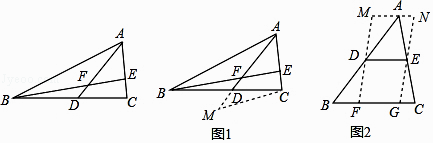
(2)解决问题:如图2,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FE、GE的延长线交于M、N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
观察:下面这些几何体都是简单几何体,请您仔细观察.
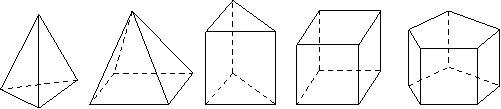
![]()
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体 | a | b | c | d | e |
棱数(E) | 6 | 9 | 15 | ||
面数(F) | 4 | 5 | 5 | 6 | |
顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,![]() ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点,所以有2![]() 3
3![]() .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有 条棱, 个顶点,每个顶点处有 条棱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com