
【题目】如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
(1)a= ,b= .
(2)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
![]()
【答案】(1)﹣8;4;(2)①t为1.6秒或8秒时,2OP﹣OQ=4;②点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.
【解析】
(1)由AO=2OB可知,将12平均分为3份,其中AO占两份为8,BO占一份为4,同时注意A点在原点左侧,B点在原点右侧;
(2)①先确定停止运动的时间,再分点P在原点左侧和右侧两种情况讨论;②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为t秒,列式2t-t=8求解即可.
(1)∵AB=12,AO=2OB,
∴AO=8,OB=4,
∴A点所表示的实数为﹣8,B点所表示的实数为4,
∴a=﹣8,b=4.
故答案是:﹣8;4;
(2)①当点P与点Q重合时,如图,
![]()
2t=12+t,t=12,
则,当0<t<4时,如图,
![]()
AP=2t,OP=8﹣2t,BQ=t,OQ=4+t,
∵2OP﹣OQ=4,
∴2(8﹣2t)﹣(4+t)=4,
t=![]() =1.6,
=1.6,
当4<t<12时,如图,
![]()
OP=2t﹣8,OQ=4+t,
则2(2t﹣8)﹣(4+t)=4,解得t=8,
综上所述,当t为1.6秒或8秒时,2OP﹣OQ=4;
②当点P到达点O时,8÷2=4,此时,OQ=4+t=8,即点Q所表示的实数为8,如图,
![]()
设点M运动的时间为t秒,
由题意得:2t﹣t=8,解得t=8,
此时,点P表示的实数为8×2=16,所以点M表示的实数也是16,
∴点M行驶的总路程为:3×8=24,
答:点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( ) 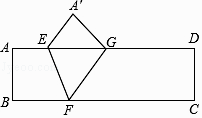
A.![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形OABC中,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0),则第二次碰到长方形的边上一点P2的坐标为________.当点P第2018次碰到长方形的边时,点P2018的坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系xOy中,正比例函数y= ![]() x的图像经过点A,点A的纵坐标为6,反比例函数y=
x的图像经过点A,点A的纵坐标为6,反比例函数y= ![]() 的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: 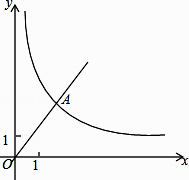
(1)这个反比例函数的解析式;
(2)直线AB(一次函数)的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)求2*(﹣2)的值;
(2)若2*x=m,![]() (其中x为有理数),试比较m,n的大小;
(其中x为有理数),试比较m,n的大小;
(3)若[![]() ]
]![]() =a+4,求a的值.
=a+4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
(1)建立适当的直角坐标系,并写出各个顶点的坐标.
(2)将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
(3)将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com