
【题目】如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( ) 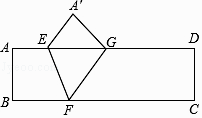
A.![]()
B.2 ![]()
C.![]()
D.![]()
【答案】C
【解析】解:作GM⊥BC于M,如图所示: 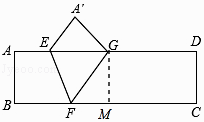
则GM=AB=1,DG=CM,
∵四边形ABCD是矩形,
∴BC=AD=4,AD∥BC,
∴∠GEF=∠BFE,
由折叠的性质得:GF=BF,∠GFE=∠BFE,
∴∠GEF=∠GFE,
∴EG=FG=BF,
设EG=FG=BF=x,
∵G是AD的中点,∴CM=DG= ![]() AD=2,
AD=2,
∴FM=BC﹣BF﹣CM=2﹣x,
在Rt△GFM中,由勾股定理得:FG2=FM2+GM2 ,
即x2=(2﹣x)2+12 ,
解得:x= ![]() ,即EG=
,即EG= ![]() ;
;
故选:C.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )

A. 45° B. 50° C. 60° D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
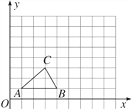
【题目】如图,在9×9网格中,每个小方格的边长看作单位1,每个小方格的顶点叫作格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C,使两个图形以点C为位似中心,且所画图形与△ABC的相似比为2∶1;
(2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C,画出图形,并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )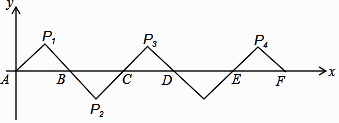
A.(4030,1)
B.(4029,﹣1)
C.(4033,1)
D.(4031,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图像提供信息,解答下列问题. 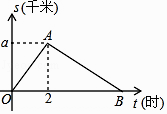
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时. ①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
A.7米
B.7.2米
C.9.7米
D.15.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
(1)a= ,b= .
(2)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com