练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲、乙两人参加学校组织的理化实验操作测试，近期的5次测试成绩如图所示．

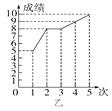
    (1)请你根据图中的数据填写表格；

    姓名

    平均数

    众数

    方差

    甲

    8

    乙

    8

    2.8

    (2)从平均数和方差相结合看，谁的成绩好些？从发展趋势来看，谁的成绩好些？

    【答案】(1)8 0.4 8；(2)从平均数和方差相结合看，甲的成绩好些；从发展趋势来看，乙的成绩好些．

    【解析】（1）直接结合图中数据结合平均数以及方差求法分别得出答案；
    （2）利用方差反映数据稳定性平均数是反映整体的平均水平进而分析得出答案．

    (1)如图所示：乙的平均数为：

    S2甲=

    =0.4；

    由图中数据可得：甲组数据的众数为8，

    姓名

    平均数

    众数

    方差

    甲

    8

    8

    0.4

    乙

    8

    8

    2.8

    (2)从平均数和方差相结合看，甲的成绩好些；

    从发展趋势来看，乙的成绩好些．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1的7张长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）

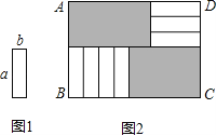
    A. a=b B. a=2b

    C. a=3b D. a=4b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后，将其裁成四个相同的等腰梯形（如图1），然后拼成一个平行四边形（如图2）。那么通过计算两个图形的阴影部分的面积，可以验证成立的公式是（ ）

    A．a2－b2=(a－b)2

    B．(a+b)2="a+2ab+b"

    C．(a－b)2=a2－2ab+b2

    D．a2－b2=(a－b)(a+b)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，将一张正方形纸片剪成四个大小一样的小正方形，然后将其中一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去。

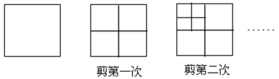
    (1)完成下表：

    剪的次数

    1

    2

    3

    4

    5

    ...

    n

    小正方形的个数

    4

    7

    10

    ...

    （2） .（用含n的代数式表示）

    （3）按上述方法，能否得到2018个小正方形？如果能，请求出n;如不能，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据题意解答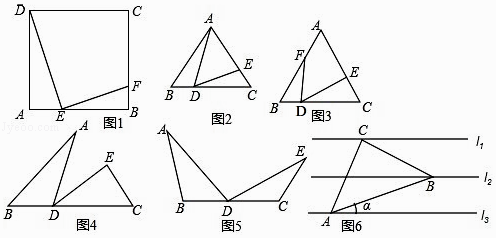

    （1）如图1，已知E是矩形ABCD的边AB上一点，EF⊥DE交BC于点F，证明：△ADE∽△BFE．
    （2）这个相似的基本图形像字母K，可以称为“K”型相似，但更因为图形的结构特征是一条线上有3个垂直关系，也常被称为“一线三垂直”，那普通的3个等角又会怎样呢？
    变式一如图2，已知等边三角形ABC，点D、E分别为BC，AC上的点，∠ADE=60°．
    ①图中有相似三角形吗？请说明理由．
    ②如图3，若将∠ADE在△ABC的内部（∠ADE两边不与BC重合），绕点D逆时针旋转一定的角度，还有相似三角形吗？
    （3）变式二如图4，隐藏变式1图形中的线段AE，在得到的新图形中．
    ①如果∠B=∠C=∠ADE=50°，图中有相似三角形吗？请说明理由．
    ②如图5，若∠B=∠C=∠ADE=∠a，∠a为任意角，还有相似三角形吗？
    （4）交式三已知，相邻两条平形直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则cosa的值是（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设边长为3的正方形的对角线长为a．下列关于a的四种说法： ①a是无理数；
    ②a可以用数轴上的一个点来表示；
    ③3＜a＜4；
    ④a是18的算术平方根．
    其中，所有正确说法的序号是（ ）
    A.①④
    B.②③
    C.①②④
    D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是王老师在数学课堂上给同学们出的一道数学题，要求对以下实数进行分类填空：

    －，0，，，18，，，－0.56，3.14159，，，，0.8080080008…，－.

    (1)有理数集合：________________________________________________________________________；

    (2)无理数集合：________________________________________________________________________；

    (3)非负整数集合：________________________________________________________________________；

    (4)分数集合：________________________________________________________________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，点A为半圆O直径MN所在直线上一点，射线AB垂直于MN，垂足为A，半圆绕M点顺时针转动，转过的角度记作a；设半圆O的半径为R，AM的长度为m，回答下列问题：
    （1）探究：若R=2，m=1，如图1，当旋转30°时，圆心O′到射线AB的距离是；如图2，当a=°时，半圆O与射线AB相切；
    （2）如图3，在（1）的条件下，为了使得半圆O转动30°即能与射线AB相切，在保持线段AM长度不变的条件下，调整半径R的大小，请你求出满足要求的R，并说明理由．
    （3）发现：如图4，在0°＜α＜90°时，为了对任意旋转角都保证半圆O与射线AB能够相切，小明探究了cosα与R、m两个量的关系，请你帮助他直接写出这个关系；cosα=（用含有R、m的代数式表示）
    （4）拓展：如图5，若R=m，当半圆弧线与射线AB有两个交点时，α的取值范围是 ， 并求出在这个变化过程中阴影部分（弓形）面积的最大值（用m表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，经过点A作AE⊥OC，垂足为点D，AE与BC交于点F，与过点B的直线交于点E，且EB=EF．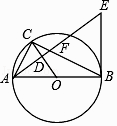
    （1）求证：BE是⊙O的切线；
    （2）若CD=1，cos∠AEB= ，求BE的长．

    查看答案和解析>>

    同步练习册答案