
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

【答案】(1)证明见解析;(2)边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
【解析】试题分析:(1)由正方形可得EH∥BC,所以可以得到对应的两组角相等,即可证明相似;(2)设正方形边长为x,再由△AEH∽△ABC得到对应边成比例,列出关于x的方程,解出x即可.
试题解析:
(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC;
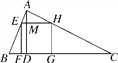
(2)解:∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM.设正方形EFGH的边长为xcm,∵△AEH∽△ABC,∴ ![]() ,∴
,∴![]() ,解得x=
,解得x=![]() .
.
∴正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
点睛:两个三角形的相似比等于对应的高之比,角平分线之比,中线之比.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 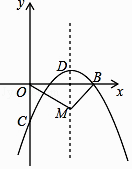
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 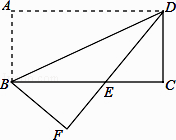
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数 | 图形 | 最多剪出的小三角形个数 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
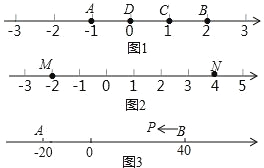
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x2y﹣3xy2+2x2y﹣y2x ;(2)2(2a2﹣9b)﹣3(3a2﹣7b);
(3)2a2﹣[![]() (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣![]() ab.
ab.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com