
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 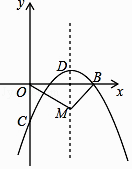
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
【答案】
(1)解:∵抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,
∴ ![]() ,
,
解得: 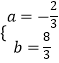 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)解:∵y=﹣ ![]() x2+
x2+ ![]() x﹣2=﹣
x﹣2=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,
,
∴D(2, ![]() ),
),
设M(2,m),
∵O( 0,0),B(3,0),
∵∠OMB=90°,
∴OM2+BM2=OB2,
即m2+22+(3﹣2)2+m2=9,
∴m= ![]() ,
,
∵ ![]() >
> ![]() ,
,
∴M(2,﹣ ![]() ),
),
∴DM= ![]() +
+ ![]() ,
,
∴t= ![]() +
+ ![]()
【解析】(1)把A(1,0)、B(3,0)代入y=ax2+bx﹣2,即可得到结果;(2)由y= ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,得到D(2,
,得到D(2, ![]() ),设M(2,m),根据勾股定理列方程得到M(2,﹣
),设M(2,m),根据勾股定理列方程得到M(2,﹣ ![]() ),于是得到结论.
),于是得到结论.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点![]() 作
作![]() ,交对角线
,交对角线![]() 于点
于点![]() .点
.点![]() 从点
从点![]() 出发,沿对角线
出发,沿对角线![]() 向点
向点![]() 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位. ![]() 、
、![]() 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为![]() 秒(
秒(![]() ).
).
(1)当![]() 时,求出
时,求出![]() 的值;
的值;
(2)连接![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
(3)试探究:当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?


查看答案和解析>>
科目:初中数学 来源: 题型:
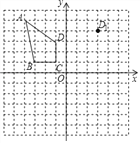
【题目】如图所示,在网格中建立平面直角坐标系,每个小正方形的边长都是1个单位长度,四边形ABCD的各顶点均在网格点上.
(1)将四边形ABCD平移,使得D点平移到D1(3,4),画出平移后的四边形A1B1C1D1;
(2)画出四边形ABCD绕着原点O逆时针旋转90°后的四边形A2B2C2D2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长. 例如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D,若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B,…设游戏者从圈A起跳.
(1)若随机掷一次骰子,求落回到圈A的概率P1;
(2)若随机掷两次骰子,用列表法或树状图法求出最后落回到圈A的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )
x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )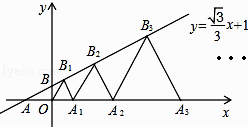
A.2n ![]()
B.(2n+1) ![]()
C.(2n﹣1﹣1) ![]()
D.(2n﹣1) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
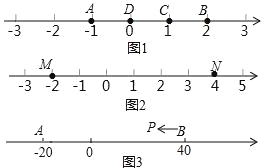
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
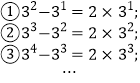
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com