
【题目】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S= .

【答案】(1)见解析;(2)S= 50.
【解析】
(1)因为BD⊥l,AE⊥l,可得∠AEC=∠CDB,结合题意得到∠CAE=∠BCD,再根据AAS证明即可.
(2)利用(1)中结论,根据全等三角形的性质进行计算即可解决问题.
(1)如图1中,
∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∴∠BCD+∠ACE=90°,
∴∠CAE=∠BCD,
在△AEC和△CDB中
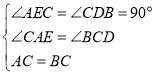 ,
,
∴△AEC≌△CDB(AAS).
(2)如图2中,因为AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,
由(1)可知:△EFA≌△AGB,△BGC≌△CHD,
∴EF=AG=6,AF=BG=CH=3,CG=DH=4,
∴S=![]() (6+4)×16-18-12=50.
(6+4)×16-18-12=50.
故答案为50.


科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费”两部分组成.为了鼓励市民节约用水, 其中城市供水费按阶梯式计费:一个月用水 10 吨以内(包括 10 吨)的用户,每吨收 1.5 元;一个月用水超过 10 吨的用户,10 吨水仍按每吨 1.5 元收费,超过 10 吨的部分,按每吨 2 元收费.另外污水处理费按每吨 0.65 元收取.
(1)某居民 5 月份用水 8 吨,应交水费多少元?
(2)某居民 6 月份用水 12 吨,应交水费多少元?
(3)若某户某月用水 x 吨,请你用含有 x 的代数式表示该月应交的水费
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示是一枚质地均匀的骰子.骰子有六个面并分别代表数字1,2,3,4,5,6.如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的点数是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落到圈F……
设游戏者从圈A起跳.
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2,并指出他与小明落回到圈A的可能性一样吗?
 图1
图1 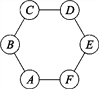 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
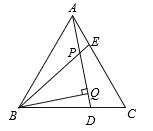
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
2, 4, 8, 16, 32, 64, …;①
0, 6, 6, 18, 30, 66, …;②
1, 2, 4, 8, 16, 32, …;③
(1)分别写出每一行的第![]() 个数;
个数;
(2)取每行数的第![]() 个数,使这三个数的和为162,求
个数,使这三个数的和为162,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
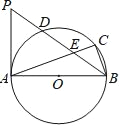
【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙两座仓库分别有农用车![]() 辆和
辆和![]() 辆,现需要调往
辆,现需要调往![]() 县
县![]() 辆, 调往
辆, 调往![]() 县
县![]() 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从甲仓库调往
元,从甲仓库调往![]() 县农用车
县农用车![]() 辆.
辆.
![]() 甲仓库调往
甲仓库调往![]() 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往![]() 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含![]() 的代数式表示);
的代数式表示);
![]() 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到![]() 、
、![]() 两县所需要的总运费(用含
两县所需要的总运费(用含![]() 的代数式表示);
的代数式表示);
![]() 在
在![]() 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
![]() 县农用车多少辆?
县农用车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
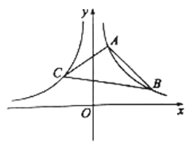
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
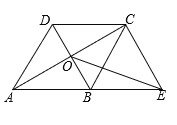
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com