
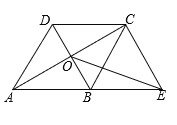
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
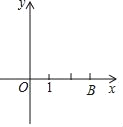
查看答案和解析>>
科目:初中数学 来源: 题型:
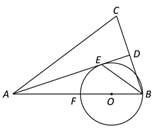
【题目】已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E, F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:“熟练工人每月工资至少3800元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资,且加工1件A型服装计酬20元,加工1件B型服装计酬15元”. (工人月工资=底薪+计件工资)在实际工作中发现一名熟练工加工1件A型服装的时间是加工1件B型服装的2倍,且工作5天(即40小时)单独加工B服装的件数比单独加工A服装的件数多20件.
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
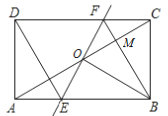
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
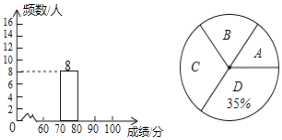
【题目】某市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题.
组别 | 成绩x/分 | 频数 |
A组 |
| a |
B组 |
| 8 |
C组 |
| 12 |
D组 |
| 14 |
(1)一共抽取了_____个参赛学生的成绩;表中![]() ____;
____;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)某校共有2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
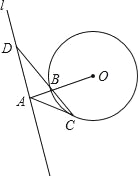
【题目】如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
(1)求证:AC是⊙O的切线;
(2)若BD=2![]() ,OA=4,求线段BC的长.
,OA=4,求线段BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com