
【题目】已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E, F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC= ![]() ,求⊙O的半径.
,求⊙O的半径.
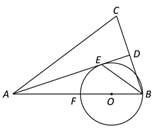
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OE;先证明OE∥BC,得出∠AEO=∠ADB,再证明AD⊥BC,得出∠AEO=90°,OE⊥AD,即可得出结论;
(2)先求出![]() ,再证明
,再证明![]() ,得出对应边成比例,即可求出半径.
,得出对应边成比例,即可求出半径.
试题解析:(1)证明:连接OE,则OE=OB,
∴∠1=∠2,
∵BE平分∠ABC,∴∠1=∠3,
∴∠2=∠3,∴OE∥BC,
∴∠AEO=∠ADB,
在△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC,∴∠ADB=90°,
∴∠AEO=90°,∴OE⊥AD,
∴AD是⊙O的切线.
(2)在△ABC中,AB=AC,AD平分∠BAC,
∴![]()
∵![]()
在△ABD中,∠ADB=90°,∴![]()
设⊙O的半径为r,则AO=6-r.
∵OE∥BC,∴△AOE∽△ABD,
∴![]() 即
即 ![]()
解得![]()
∴⊙O的半径为![]()


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
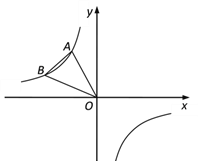
【题目】如图,点A、B在反比例函数y=- ![]() 的图象上,且点A、B的横坐标分别为a、2a(a<0).
的图象上,且点A、B的横坐标分别为a、2a(a<0).
(1)求△AOB的面积;
(2)若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示),
![]()
(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②![]() 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
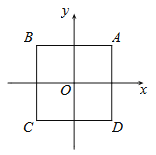
【题目】如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
(1)若函数y=x2+m的图象过点C,求这个函数的解析式;并判断其函数图象是否过A点.
(2)若将(1)中的函数图象先向右平移1个单位,再向上平移2个单位,直接写出平移后函数的解析式和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
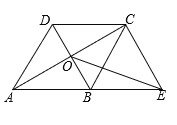
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com