
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
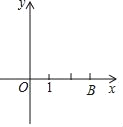
【答案】(1)抛物线的解析式为y=x2﹣4x+3;(2)S△DBC=3;(3)F(0,﹣![]() ).
).
【解析】试题分析:
(1)由题意可设平移后的直线的解析式为y=kx+3,代入点B的坐标可求得k的值,从而可得直线BC的解析式y=-x+3,由此可解得点C的坐标,将B、C的坐标代入抛物线的解析式列方程组可求得b、c的值,即可得到抛物线的解析式;
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴,由(1)中所得抛物线的解析式求出其顶点D的坐标即可由S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE求出其面积了;
(3)如图2所示:过点F作FG⊥CD,垂足为G.由(1)(2)易得CD=![]() ,tan∠OCD=tan∠GCF=
,tan∠OCD=tan∠GCF=![]() ,则CG=2FG,由∠GCF=45°,∠FGD=90°可得△FGD为等腰直角三角形,由此可得FG=GD,由此可得CD=3FG,则FG=
,则CG=2FG,由∠GCF=45°,∠FGD=90°可得△FGD为等腰直角三角形,由此可得FG=GD,由此可得CD=3FG,则FG=![]() ,CG=
,CG=![]() ,从而在Rt△CFG中,可得CF=
,从而在Rt△CFG中,可得CF=![]() ,则OF=CF﹣OC=
,则OF=CF﹣OC=![]() ,就可得到点F的坐标为(0,﹣
,就可得到点F的坐标为(0,﹣![]() ).
).
试题解析:
(1)将直线y=kx(k≠0)沿着y轴向上平移3个单位长度,所得直线的解析式为y=kx+3,
将点B(3,0)代入得:3k+3=0,解得k=﹣1,
∴直线BC的解析式为y=﹣x+3.
令x=0得:y=3,
∴C(0,3).
将B(3,0),C(0,3)代入抛物线的解析式得:![]() ,解得:b=﹣4,c=3,
,解得:b=﹣4,c=3,
∴抛物线的解析式为y=x2﹣4x+3.
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴.
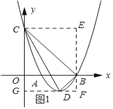
y=x2﹣4x+3=(x﹣2)2﹣1.
∴D(2,﹣1).
∴S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE=12﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1﹣
×1×1﹣![]() ×3×3=3.
×3×3=3.
(3)如图2所示:过点F作FG⊥CD,垂足为G,由(1)(2)易得CD=![]() ,
,
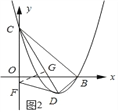
∵C(0,3),D(2,﹣1),
∴CD=![]() ,
,
∵tan∠OCD=tan∠GCF=![]() ,
,
∴CG=2FG.
又∵∠GCF=45°,∠FGD=90°,
∴△FGD为等腰直角三角形,
∴FG=GD.
∴CD=3FG,
∴FG=![]() .
.
∴CG=2FG=![]() .
.
∴在Rt△CFG中,依据勾股定理可知:CF=![]() .
.
∴OF=CF﹣OC=![]() .
.
∴F(0,﹣![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
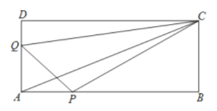
【题目】在长方形ABCD中,AB=3a厘米,BC=a厘米,点P沿AB边从点A开始向终点B以2厘米/秒的速度移动,点Q沿DA边从点D开始向终点A以1厘米/秒的速度移动,如果P、Q同时出发,以t(秒)表示移动的时间,
(1)用含有a、t的代数式表示△APC的面积
(2)求△PQC的面积(用含有a、t的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
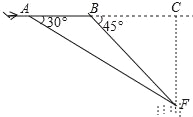
【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列解题过程:
计算:1+5+52+53+…+524+525的值.
解:设S=1+5+52+53+…+524+525,(1)
则5S=5+52+53+…+525+526(2)
(2)﹣(1),得4S=526﹣1
S=![]()
通过阅读,你一定学会了一种解决问题的方法,请用你学到的方法计算:
(1)1+3+32+33+…+39+310
(2)1+x+x2+x3+…+x99+x100.
查看答案和解析>>
科目:初中数学 来源: 题型:
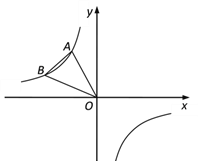
【题目】如图,点A、B在反比例函数y=- ![]() 的图象上,且点A、B的横坐标分别为a、2a(a<0).
的图象上,且点A、B的横坐标分别为a、2a(a<0).
(1)求△AOB的面积;
(2)若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示),
![]()
(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②![]() 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
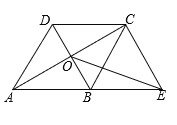
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
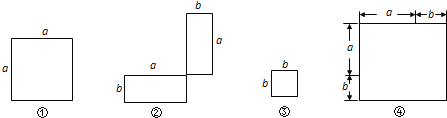
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达:.
(3)利用(2)的结论计算10.232+20.46×9.77+9.772的值.(写出计算过程)
(4)已知M=-2x2-3x-6, N=-3x2-5x-7,利用(2)的结论,求M与N的大小关系为( )
A. M>N B. M<N C. M≥N D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com