
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
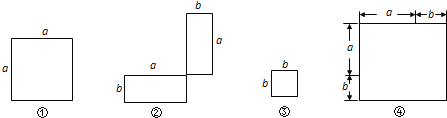
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达:.
(3)利用(2)的结论计算10.232+20.46×9.77+9.772的值.(写出计算过程)
(4)已知M=-2x2-3x-6, N=-3x2-5x-7,利用(2)的结论,求M与N的大小关系为( )
A. M>N B. M<N C. M≥N D.不能确定
【答案】(1)①a2; ②2ab;③b2;④(a+b)2;(2) a2+2ab+b2=(a+b)2;(3) 400;(4)C
【解析】
(1)根据正方形、长方形面积公式即可解答;(2)前三个图形的面积之和等于第四个正方形的面积;(3)借助于完全平方公式解答即可;(4)用作差法比较大小.
解:(1)①边长为a的正方形面积为a2;
②两个长和宽分别为a和b的长方形面积为2ab;
③边长为b的正方形面积为b2;
④边长为a+b的正方形面积为(a+b)2;
(2)前三个图形的面积之和等于第四个正方形的面积
∴a2+2ab+b2=(a+b)2;
(3)10.232+20.46×9.7+9.72=![]()
(4)M- N =-2x2-3x-6-(-3x2-5x-7)=-2x2-3x-6+3x2+5x+7=![]() ,
,
∴M≥N
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
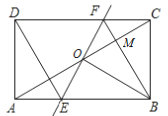
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
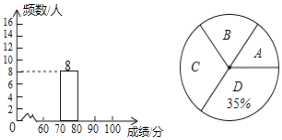
【题目】某市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题.
组别 | 成绩x/分 | 频数 |
A组 |
| a |
B组 |
| 8 |
C组 |
| 12 |
D组 |
| 14 |
(1)一共抽取了_____个参赛学生的成绩;表中![]() ____;
____;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)某校共有2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
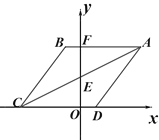
【题目】如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)探索规律观察下面由※组成的图案和算式,解答问题

(1)请计算1+3+5+7+9+11=__________;
(2)请猜想1+3+5+7+9+…+19=__________;
(3)请猜想1+3+5+7+9+…+(2n﹣1)=__________;
(4)请用上述规律计算:21+23+25+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=2,BC=4.点D是线段BC上的一个动点.点D与点B、C不重合,过点D作DE⊥BC交AB于点E,将△ABC沿着直线DE翻折,使点B落在直线BC上的F点.
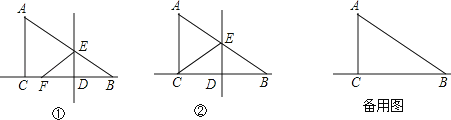
(1)设∠BAC=α(如图①),求∠AEF的大小;(用含α的代数式表示)
(2)当点F与点C重合时(如图②),求线段DE的长度;
(3)设BD=x,△EDF与△ABC重叠部分的面积为S,试求出S与x之间函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
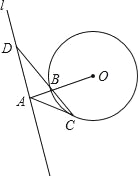
【题目】如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
(1)求证:AC是⊙O的切线;
(2)若BD=2![]() ,OA=4,求线段BC的长.
,OA=4,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com