
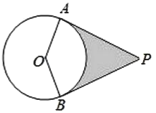
【题目】如图,![]() 的半径为4,过圆外一点
的半径为4,过圆外一点![]() 画
画![]() 的两条切线
的两条切线![]() 和
和![]() ,
,![]() 、
、![]() 为切点,若
为切点,若![]() ,则阴影部分的面积是__________.(结果保留
,则阴影部分的面积是__________.(结果保留![]() )
)
【答案】![]()
【解析】
连接OP,如图,根据切线的性质和切线长定理得到∠PAO=∠PBO=90°,∠APO=30°,则根据四边形内角和得到∠AOB=180°-∠APB=120°,再在Rt△PAO中利用含30度的直角三角形三边的关系得到![]() ,则
,则![]() ,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
连接OP,如图,
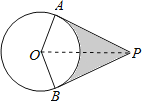
∵PA,PB是⊙O的两条切线,
∴OA⊥AP,OB⊥PB,OP平分∠APB,
∴∠PAO=∠PBO=90°, ![]() ,
,
∴∠AOB=180°-∠APB=180°-60°=120°,
在Rt△PAO中,∵OA=4,∠APO=30°,
∴![]() ,
,
∴![]() ,
,
∴阴影部分的面积![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
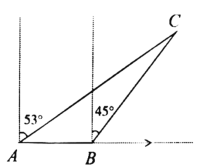
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .抛物线
.抛物线![]() 过
过![]() 、
、![]() 两点.
两点.
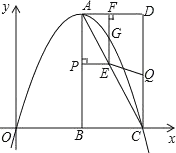
(1)直接写出点![]() 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
(2)动点![]() 从点
从点![]() 出发.沿线段
出发.沿线段![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动.速度均为每秒1个单位长度,运动时间为
运动.速度均为每秒1个单位长度,运动时间为![]() 秒.过点
秒.过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
①过点![]() 作
作![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .当
.当![]() 为何值时,线段
为何值时,线段![]() 最长?
最长?
②连接![]() .在点
.在点![]() 、
、![]() 运动的过程中,判断有几个时刻使得
运动的过程中,判断有几个时刻使得![]() 是等腰三角形?请直接写出相应的
是等腰三角形?请直接写出相应的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
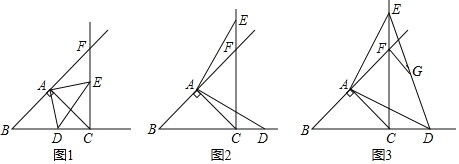
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(不与点B、点C重合),将线段AD绕A逆时针旋转90°得到线段AE,作射线BA与射线CE,两射线交于点F.
(1)若点D在线段BC上,如图1,请直接写出CD与EF的关系.
(2)若点D在线段BC的延长线上,如图2,(1)中的结论还成立吗?请说明理由.
(3)在(2)的条件下,连接DE,G为DE的中点,连接GF,若tan∠AEC=![]() ,AB=
,AB=![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
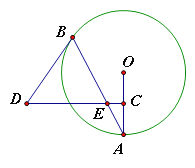
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
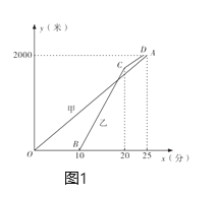
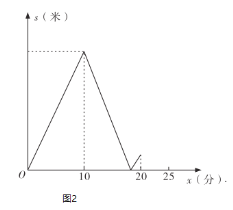
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com