
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
【答案】(1)30辆;(2)该出租公司的日租金总收入最高是8000元,当日租金总收入最高时,每天出租货车20辆
【解析】
(1)根据题意可以列出分式方程,解分式方程进而求得答案;
(2)根据题意可以求得总收入和上涨价格之间的函数解析式,然后化为顶点式即可解答.
解:(1)该出租公司这批对外出租的货车共有x辆,
根据题意得,![]() ×(1+25%)
×(1+25%)![]() ,
,
解得:![]() ,
,
经检验:![]() 是分式方程的解,且符合题意,
是分式方程的解,且符合题意,
答:该出租公司这批对外出租的货车共有30辆;
(2)设旺季每辆货车的日租金上涨![]() 元时,则每天出租货车(
元时,则每天出租货车(![]() )辆,该出租公司的日租金总收入为W元,
)辆,该出租公司的日租金总收入为W元,
根据题意得:
W=![]() ,
,
∵![]() <0,
<0,
∴当![]() 时,W有最大值为8000元,此时
时,W有最大值为8000元,此时![]() ;
;
答:该出租公司的日租金总收入最高是8000元,当日租金总收入最高时,每天出租货车20辆.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为_____.
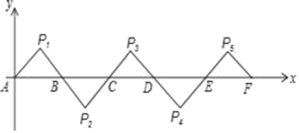
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,点
,点![]() 是点
是点![]() 以
以![]() 为对称中心的对称点,点
为对称中心的对称点,点![]() 运动的同时,点
运动的同时,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,当点
,当点![]() 到达顶点
到达顶点![]() 时,
时,![]() 同时停止运动,设
同时停止运动,设![]() 两点运动时间为
两点运动时间为![]() 秒.
秒.
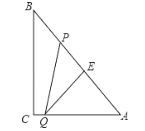
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)四边形![]() 面积能否是
面积能否是![]() 面积的
面积的![]() ?若能,求出此时
?若能,求出此时![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() 为等腰三角形?(直接写出结果)
为等腰三角形?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=﹣x﹣6与x轴,y轴分别交于点A,B将直线AB沿y轴正方向平移与反比例函数y=![]() (x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(1)求直线AC和反比例函数的解析式;
(2)连接AD,求△ACD的面积.
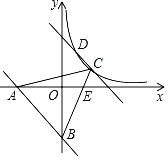
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:
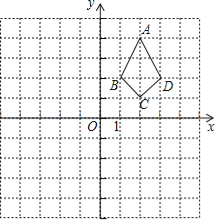
(1)将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;
(2)将四边形A1B1C1D1绕点A1逆时针旋转90°,得到四边形A1B2C2D2,画出旋转后的四边形A1B2C2D2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com