
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的弦,且
的弦,且![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
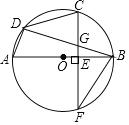
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据点![]() 为
为![]() 的中点和垂径定理可证CD=BF,再利用
的中点和垂径定理可证CD=BF,再利用![]() 即可证得结论;
即可证得结论;
(2)解法一:连接![]() ,设
,设![]() 的半径为
的半径为![]() ,由
,由![]() 列出关于
列出关于![]() 的方程就能求解;
的方程就能求解;
解法二:如图,作辅助线,构建角平分线和全等三角形,证明![]() ,得
,得![]() ,再证明
,再证明![]() ,得
,得![]() ,进而可得
,进而可得![]() 和
和![]() 的长,易证
的长,易证![]() ,列比例式可求得
,列比例式可求得![]() 的长,也就是
的长,也就是![]() 的长;
的长;
解法三:连接![]() ,根据垂径定理和三角形的中位线定理可得
,根据垂径定理和三角形的中位线定理可得![]() ,再证明
,再证明![]() ,然后利用勾股定理即可求出结果.
,然后利用勾股定理即可求出结果.
证明:(1)∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 是
是![]() 的直径,且
的直径,且![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ;
;
(2)解法一:如图,连接![]() ,设
,设![]() 的半径为
的半径为![]() ,
,
![]() 中,
中,![]() ,即
,即![]() ,
,
![]() 中,
中,![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() (舍)或3,
(舍)或3,
∴![]() ,
,
∴![]() ;
;

解法二:如图,过![]() 作
作![]() 交AD延长线于点
交AD延长线于点![]() ,连接
,连接![]() 、
、![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

解法三:如图,连接![]() ,交
,交![]() 于
于![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
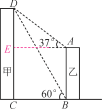
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
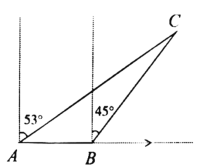
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
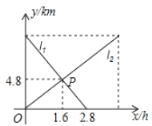
【题目】小敏从![]() 地出发向
地出发向![]() 地行走,同时小聪从
地行走,同时小聪从![]() 地出发向
地出发向![]() 地行走,如图,相交于点
地行走,如图,相交于点![]() 的两条线段
的两条线段![]() 分别表示小敏、小聪离
分别表示小敏、小聪离![]() 地的距离
地的距离![]() 与已用时间
与已用时间![]() 之间的关 系,则
之间的关 系,则![]() _______时,小敏、小聪两人相距
_______时,小敏、小聪两人相距![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
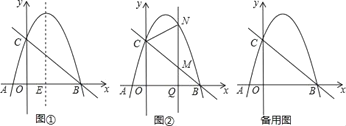
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .抛物线
.抛物线![]() 过
过![]() 、
、![]() 两点.
两点.
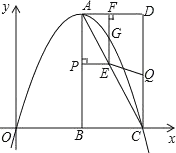
(1)直接写出点![]() 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
(2)动点![]() 从点
从点![]() 出发.沿线段
出发.沿线段![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动.速度均为每秒1个单位长度,运动时间为
运动.速度均为每秒1个单位长度,运动时间为![]() 秒.过点
秒.过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
①过点![]() 作
作![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .当
.当![]() 为何值时,线段
为何值时,线段![]() 最长?
最长?
②连接![]() .在点
.在点![]() 、
、![]() 运动的过程中,判断有几个时刻使得
运动的过程中,判断有几个时刻使得![]() 是等腰三角形?请直接写出相应的
是等腰三角形?请直接写出相应的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com