
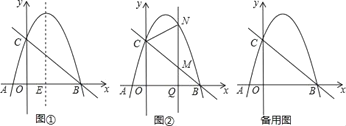
����Ŀ����ͼ����֪������y=ax2��3ax��4a(a��0)��ͼ����x�ύ��A��B����(A��B�����)����y�������ύ�ڵ�C������BC�����κ����ĶԳ�����x��Ľ���ΪE��
(1)�����ߵĶԳ�����x��Ľ���E����Ϊ_____����A������Ϊ_____��
(2)����EΪԲ�ĵ�Բ��y���ֱ��BC�����У�����������ߵĽ���ʽ��
(3)��(2)�������£���ͼ��Q(m��0)��x����������һ�㣬����Q��y���ƽ���ߣ���ֱ��BC���ڵ�M���������߽��ڵ�N������CN������CMN��CN���ۣ�M�Ķ�Ӧ��ΪM������ͼ����̽�����Ƿ���ڵ�Q��ʹ��M��ǡ������y���ϣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)E(![]() ��0)��A(��1��0)��(2)y=
��0)��A(��1��0)��(2)y=![]() ��(3)���ڣ���Q����Ϊ(
��(3)���ڣ���Q����Ϊ(![]() ��0)��(
��0)��(![]() ��0)
��0)
��������
��1�����ݶԳ��ṫʽ���������E���꣬��y��0���ⷽ�̼��������A���꣮
��2����ͼ���У�����E��ֱ��BC�����ڵ�D������DE����DE��BC����tan��OBC��![]() ���г����̼��ɽ����
���г����̼��ɽ����
��3����������������N��ֱ��BC�Ϸ�������N��ֱ��BC�·����ֱ��г����̼��ɽ����
�⣺(1)���Գ���x=![]() ��
��
����E����(![]() ��0)��
��0)��
��y=0������ax2��3ax��4a=0��
��x=��1��4��
����A����(��1��0)��
�ʴ𰸷ֱ�Ϊ(![]() ��0)��(��1��0)��
��0)��(��1��0)��
(2)��ͼ���У�����E��ֱ��BC�����ڵ�D������DE����DE��BC��

��DE=OE=![]() ��EB=
��EB=![]() ��OC=��4a��
��OC=��4a��
��DB=![]() ��
��
��tan��OBC=![]() ��
��
��![]() �����a=
�����a=![]() ��
��
�������߽���ʽΪy=![]() ��
��
(3)��ͼ���У���������M��CN=��NCB��

��MN��OM����
���M��CN=��CNM��
��MN=CM��
����B������Ϊ(4��0)����C������Ϊ(0��3)��
�� ֱ��BC����ʽΪy=��![]() x+3��BC=5��
x+3��BC=5��
��M(m����![]() m+3)��N(m����
m+3)��N(m����![]() m2+
m2+![]() m+3)����MF��OC��F��
m+3)����MF��OC��F��
��sin��BCO=![]() ��
��
��![]() ��
��
��CM=![]() m��
m��
����N��ֱ��BC�Ϸ�ʱ����![]() m2+
m2+![]() m+3��(��
m+3��(��![]() m+3)=
m+3)=![]() m��
m��
��ã�m=![]() ��0(����)��
��0(����)��
��Q1(![]() ��0)��
��0)��
����N��ֱ��BC�·�ʱ��(��![]() m+3)��(��
m+3)��(��![]() m2+
m2+![]() m+3)=
m+3)=![]() m��
m��
���m=![]() ��0(����)��
��0(����)��
��Q2(![]() ��0)��
��0)��
������������Q����Ϊ(![]() ��0)��(
��0)��(![]() ��0)��
��0)��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
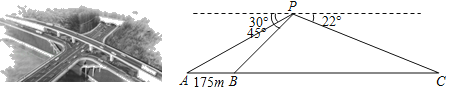
����Ŀ���������岨֮�ϵĻ�ʯ�������Ѿ���ͨ�����ɽ��������Ϊ��ʩ������Խ������������ֱ��ͨ������������ͤ�ϳ�����֪������Ů������Ϊһ�壬�����˶�ʩ������ͨӵ�µ���״����ͼ��ij��ѧ��ȤС���������˻������ɽ�������Ͽյ�P����û�ʯ�������˵�A�ĸ���Ϊ30�㣬���˵�B�����������ڣ��ĸ���Ϊ45�㣬����������C�ĸ���Ϊ22�㣬��֪��ʯ����ABȫ��175�ף�����BC�ij�Լ�����ף���������ȷ��1�ף������ο����ݣ�sin22���0.37��cos22���0.93��tan22���0.40��![]() 1.4��
1.4��![]() 1.7��
1.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
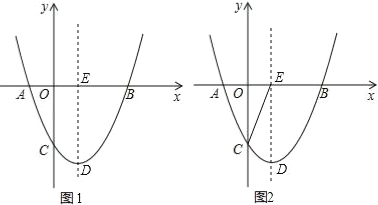
����Ŀ����ͼ1����֪���κ���y��ax2+bx+c(a��0)��ͼ����x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C(0����2)������ΪD���Գ��ύx���ڵ�E��
(1)��ö��κ����Ľ���ʽ��
(2)��MΪ�������߶Գ�������ϵ�һ�㣬����M��ֱ��MN��x�ᣬ��������������һ��N���Ƿ���ڵ�M��ʹ�ı���DMEN�����Σ������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
(3)����CE(��ͼ2)�����P��λ�ڶԳ����Ҳ����������һ�㣬����P��PQ��x�ᣬ����ΪQ������PE�����������PQE���COE����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���ң���
���ң���![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��
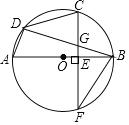
(1)��֤��![]() ��
��
(2)��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף�����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա��������գ����·ֱ���A��B��C��D��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в���������

�����������Ϣ�ش�
��1�����βμӳ�������ľ����ж����ˣ�
��2����������������ͼ����������
��3������������8000�ˣ�����ư���D�յ�������
��4������������ȫ��ͬ��A��B��C��D�ո�һ���������С���������������б�����״ͼ�ķ����������ڶ����Ե���ǡ����C�յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���ABC=120�㣬AB=10cm����P����������ڲ�����ϵ�һ�㣮����P��B��CΪ������������ǵ��������Σ���P��A��P��A���㲻�غϣ���������̾���Ϊ______cm��
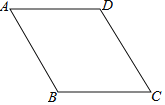
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���ABC=90����
��1���߹���ͼ��������Ҫ�������ͼ��������ͼ�ۼ����������ĸ��
�����߶�AC�Ĵ�ֱƽ����l����AC�ڵ�O��
������BO���ӳ�����BO���ӳ����Ͻ�ȡOD��ʹ��OD=OB��
������DA��DC��
��2���ж��ı���ABCD����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�A(0��0)��B(2��0)����AP1B�ǵ���ֱ�������Σ��ҡ�P1��90��������AP1B�Ƶ�B˳ʱ����ת180�����õ���BP2C������BP2C�Ƶ�C˳ʱ����ת180�����õ���CP3D���������ƣ��õ��ĵ���ֱ�������ε�ֱ�Ƕ���P2020������Ϊ_____��
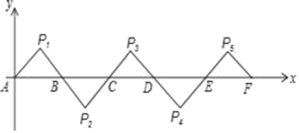
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ı���ABCD��λ����ͼ��ʾ������������⣺
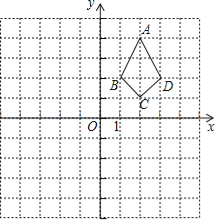
��1�����ı���ABCD������ƽ��4����λ��������ƽ��6����λ���õ��ı���A1B1C1D1������ƽ�ƺ���ı���A1B1C1D1��
��2�����ı���A1B1C1D1�Ƶ�A1��ʱ����ת90�����õ��ı���A1B2C2D2��������ת����ı���A1B2C2D2����д����C2�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com