
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.
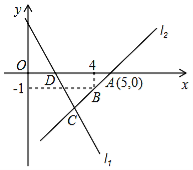
【答案】(1)直线l2的函数解析式为y=x﹣5(2)3(3)在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.
【解析】试题分析:(1)根据A、B的坐标,设直线l2的函数解析式为y=kx+b,利用待定系数发求出函数l2的解析式;
(2)由函数的解析式联立方程组,求解方程组,得到C点坐标,令y=-2x+4=0,求出D点坐标,然后求解三角形的面积;
(3)假设存在,根据两三角形面积间的关系|yP|=2|yC|,=4,再根据一次函数图像上点的坐标特征即可求出P点的坐标.
试题解析:(1)设直线l2的函数解析式为y=kx+b,
将A(5,0)、B(4,﹣1)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线l2的函数解析式为y=x﹣5.
(2)联立两直线解析式成方程组,
![]() ,解得:
,解得: ![]() ,
,
∴点C的坐标为(3,﹣2).
当y=﹣2x+4=0时,x=2,
∴点D的坐标为(2,0).
∴S△ADC=![]() AD|yC|=
AD|yC|=![]() ×(5﹣2)×2=3.
×(5﹣2)×2=3.
(3)假设存在.
∵△ADP面积是△ADC面积的2倍,
∴|yP|=2|yC|=4,
当y=x﹣5=﹣4时,x=1,
此时点P的坐标为(1,﹣4);
当y=x﹣5=4时,x=9,
此时点P的坐标为(9,4).
综上所述:在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
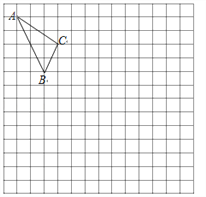
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
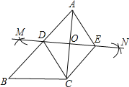
【题目】如图,已知![]() ,按如下步骤作图:
,按如下步骤作图:
①分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径在
的长为半径在![]() 两边作弧,交于两点
两边作弧,交于两点![]() 、
、![]() ;
;
②作直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
③过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 当
当![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
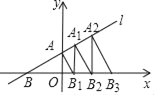
【题目】如图,在平面直角坐标系中,直线l:y=![]() x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了![]() 如图,作一个
如图,作一个![]() ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接![]() 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分![]() .
.
你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求证:OP平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
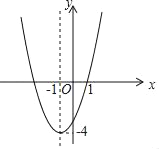
【题目】已知二次函数的图象如图所示.
(1)求这个二次函数的表达式;
(2)将该二次函数图象向上平移 个单位长度后恰好过点(﹣2,0);
(3)观察图象,当﹣2<x<1时,y的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com