练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

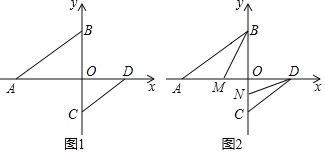
    【题目】如图1，在平面直角坐标系中，点A、B、C、D均在坐标轴上，AB∥CD．

    （1）求证：∠ABO+∠CDO＝90°；

    （2）如图2，BM平分∠ABO交x轴于点M，DN平分∠CDO交y轴于点N，求∠BMO+∠OND的值．

    【答案】（1）详见解析；（2）135°．

    【解析】

    （1）根据平行线的性质得到∠ABO＝∠DCO，然后结合等量代换证明；

    （2）根据角平分线的定义、结合（1）中结论计算．

    （1）证明：∵AB∥CD，

    ∴∠ABO＝∠DCO，

    ∵∠DCO+∠CDO＝90°；

    ∴∠ABO+∠CDO＝90°；

    （2）∵BM平分∠ABO，DN平分∠CDO，

    ∴∠MBO＝∠ABO，∠NDO＝∠CDO，

    ∴∠MBO+∠NDO＝（∠ABO+∠CDO）＝45°，

    ∴∠BMO+∠OND＝135°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

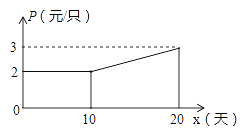
    【题目】传统的端午节即将来临，某企业接到一批粽子生产任务，约定这批粽子的出厂价为每只4元，按要求在20天内完成.为了按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足如下关系：

    y=

    （1）李明第几天生产的粽子数量为280只？

    （2）如图，设第x天生产的每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价-成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米，求旗杆的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．

    （1）求抛物线的函数表达式；

    （2）点D为直线AC上方抛物线上一动点；

    ①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1， △BCE的面积为S2， 求的最大值；

    ②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

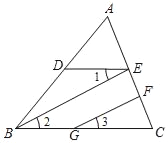
    【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．

    阅读下面的解答过程，并填空(理由或数学式)

    解：∵BE∥GF(已知)

    ∴∠2＝∠3(　 　)

    ∵∠1＝∠3(　 　)

    ∴∠1＝(　 　)(　 　)

    ∴DE∥(　 　)(　 　)

    ∴∠EDB+∠DBC＝180°(　 　)

    ∴∠EDB＝180°﹣∠DBC(等式性质)

    ∵∠DBC＝(　 　)(已知)

    ∴∠EDB＝180°﹣70°＝110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察以下等式：

    将以上三个等式两边分别相加得：

    （1）猜想并写出：____________．

    （2）直接写出下列各式的计算结果：

    ①_____________；

    ②___________．

    （3）探究并计算：

    （4）___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

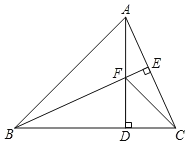
    【题目】如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF．

    （1）求证：BF=2AE；

    （2）若CD=3，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，边AB、AC的垂直平分线分别交BC于E、F，若∠EAF＝90°，AF＝3，AE＝4．

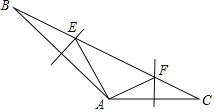
    （1）求边BC的长；（2）求出∠BAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在四边形ABCD中，AB=CD，BC=AD，E、F是对角线AC上两点，且AE=CF.求证：BE=DF．

    查看答案和解析>>

    同步练习册答案