
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
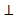
(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
【答案】(1)证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO,∴Rt△BOE≌Rt△AOF,∴OE=OF.
(2)OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,∴∠F+∠MBF=90°=∠E+∠OBE.
又∵∠MBF=∠OBE,∴∠F=∠E,
∴Rt△BOE≌Rt△AOF,∴OE=OF.
【解析】试题分析:(1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
试题解析:(1)证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.
解:OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B表示的数分别是有理数a,b.
(1)若点A在原点的左侧,点B在原点的右侧,且|a|=|b|,则a与b的关系是 ,用式子表示为 .
(2)若a=﹣5,b=1![]()
①分别写出a,b的相反数;
②求|a![]() |﹣|b
|﹣|b![]() |的值.
|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG. 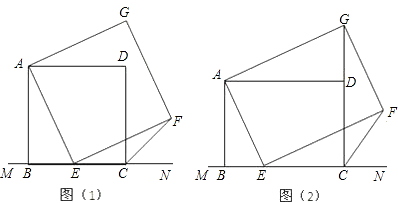
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
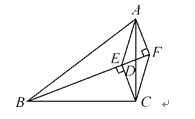
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com