
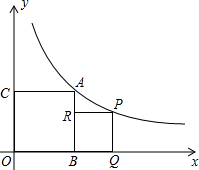
 如图,双曲线y=$\frac{k}{x}$(x>0)在第一象限内的一支,点A,P是图象上的两点,作AB⊥x轴,AC⊥y轴,PQ⊥x轴,PR⊥AB,垂足分别是B,C,Q,R,且四边形ABOC与四边形PQBR都是正方形.
如图,双曲线y=$\frac{k}{x}$(x>0)在第一象限内的一支,点A,P是图象上的两点,作AB⊥x轴,AC⊥y轴,PQ⊥x轴,PR⊥AB,垂足分别是B,C,Q,R,且四边形ABOC与四边形PQBR都是正方形.分析 (1)由k=1,利用反比例函数k的几何意义得到AC•AB=1,再由四边形ABOC为正方形,利用正方形的性质得到AC=AB,确定出A坐标,进而求出正方形ABOC的边长,设出P的坐标,将P坐标代入反比例解析式求出m的值,即为正方形PQBR的边长;
(2)由k=2,同理求出正方形ABOC与正方形PQBR的边长即可;
(3)分别求出(1)和(2)中两正方形边长之比,发现之比为$\frac{\sqrt{5}+1}{2}$,对于任意的k(k>0),同理表示出两正方形边长,求出之比即可.
解答 解:(1)当k=1时,可得AC•AB=1,
∵四边形ABOC为正方形,
∴AC=AB=1,即A(1,1),即正方形ABOC的边长为1,
设正方形PQBR的边长为m(m>0),可得P(1+m,m),
把P代入在双曲线y=$\frac{1}{x}$中,得:m(m+1)=1,
解得:m=$\frac{\sqrt{5}-1}{2}$(负值舍去),
则正方形PQBR的边长为$\frac{\sqrt{5}-1}{2}$;
(2)k=2时,同理得到A($\sqrt{2}$,$\sqrt{2}$),
设正方形PQBR边长为m(m>0),可得P($\sqrt{2}$+m,m),
把P坐标代入反比例解析式得:m(m+$\sqrt{2}$)=2,
解得:m=$\frac{\sqrt{10}-\sqrt{2}}{2}$.
则正方形PQBR边长为$\frac{\sqrt{10}-\sqrt{2}}{2}$;
(3)第(1),(2)题中的正方形ABOC与正方形PQBR的边长之比为1:$\frac{\sqrt{5}-1}{2}$=$\frac{\sqrt{5}+1}{2}$,
对于任意正数k,同理可得A($\sqrt{k}$,$\sqrt{k}$),
设正方形PQBR边长为m,可得P($\sqrt{k}$+m,m),
把P坐标代入反比例解析式得:m($\sqrt{k}$+m)=k,
整理得:m2+$\sqrt{k}$m-k=0,
解得:m=$\frac{-\sqrt{k}+\sqrt{5k}}{2}$=$\frac{\sqrt{5}-1}{2}$•$\sqrt{k}$,
∴正方形ABOC与正方形PQBR的边长之比$\sqrt{k}$:m=1:$\frac{\sqrt{5}-1}{2}$=$\frac{\sqrt{5}+1}{2}$,对于k>0时,以上结论都成立.
点评 此题属于反比例函数综合题,涉及的知识有:正方形的性质,反比例函数的图象与性质,坐标与图形性质,熟练掌握反比例函数的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
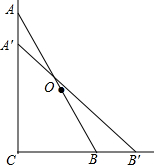 如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.
如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
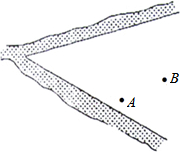 已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.
已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com