
���� ��1�����ȼ����������ס���˼�x�䣬˫�˼�y�䣬���˼�z�䣬��ס��ΪaԪ��������ĿҪ���г������飬�ֱ����y��z��x��ʾ�Ĺ�ϵʽ����0��x��20��0��y��20��0��z��20������y��z��x��ʾ�Ĺ�ϵʽ��ȷ��x��ȡֵ��Χ����y��z��ϵʽ����60x+60y+50z=a������x��a��ʾ�Ĺ�ϵʽ������x��ȡֵ�������a��ȡֵ��Χ��ȷ��a����Сֵ����ʱ�����x��ֵ������y��z����x�Ĺ�ϵʽ�������y��z��ֵ��
��2�����Ȱ��Ŵ�С���ķ���ס˫�˼䣬�����������ಡ����Ҫ��ס���˼䣬�ٰ����е�����Ů�������˼䣬�ٿ�ʣ�µ�������һ�����ŵó��𰸼��ɣ�
��� �⣺��1�����������ס���˼�x�䣬˫�˼�y�䣬���˼�z�䣬��ס��ΪaԪ��
���������$\left\{\begin{array}{l}{x+y+z=20��}\\{3x+2y+z=50��}\\{60x+60y+50z=a��}\end{array}\right.$
�ɢ�-�ٵ�2x+y=30����y=30-2x ��
�ɢ�-�١�2��x-z=10����z=x-10 ��
��0��y��20����0��30-2x��20�����5��x��15 ��
ͬ��0��z��20����0��x-10��20�����10��x��30 ��
�ɢޢ�֪10��x��15
���ܢݴ���۵�a=60x+60��30-2x��+50��x-10��=1300-10x⇒x=130-$\frac{a}{10}$
��10��130-$\frac{a}{10}$��15⇒1150��a��1200��
�������ʡ��ס������1150Ԫ����ʱx=15
�ٽ�x��ֵ����ܢݵ�y=0��z=5��
�����˼�ͷ�ס��15�䣬˫�˼�ͷ�ס��0�䣬���˼�ͷ�ס��5�䣬��ͷ�����1150Ԫ��
��2���������
4�Է���+4⇒4��˫�˼�
2���ಡ⇒2������
�е���17⇒6���˼�
Ů����13⇒5���˼�
ʣ3�Է���⇒3��˫�˼�
һ����Ҫ4+2+6+5+3=20�䣬
���� ���⿼����Ԫһ�η������Ӧ�ã��������Ĺؼ��Ǹ�����Ŀ�����飬�����x��ʾ��y��z����ʽ����������0��x��20��0��y��20��0��z��20�����x��ȡֵ��Χ������ȷ��a��ȡֵ��Χ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | Ƶ�� | Ƶ�� |
| ��Ǩ | 4 | A |
| ���Ƹ� | 7 | 0.175 |
| ���� | b | 0.2 |
| ���� | 10 | 0.25 |
| �γ� | 12 | 0.275 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
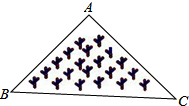 ��ͼ��ʾ����һ�������εIJ�ƺ����Ҫ�ڲ�ƺ�Ͻ�һ��ͤ�������Ϣ��Ҫʹ��ͤ����ƺ�����ߵľ�����ȣ���ͤ��λ��Ӧѡ�ڣ�������
��ͼ��ʾ����һ�������εIJ�ƺ����Ҫ�ڲ�ƺ�Ͻ�һ��ͤ�������Ϣ��Ҫʹ��ͤ����ƺ�����ߵľ�����ȣ���ͤ��λ��Ӧѡ�ڣ�������| A�� | ��ABC���������ߵĽ��� | B�� | ��ABC������ƽ���ߵĽ��� | ||
| C�� | ��ABC����������ֱ�ߵĽ��� | D�� | ��ABC���ߵ��д��ߵĽ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | 2 | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 54.32��104 | B�� | 5.432��105 | C�� | 5.432��106 | D�� | 0.5432��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
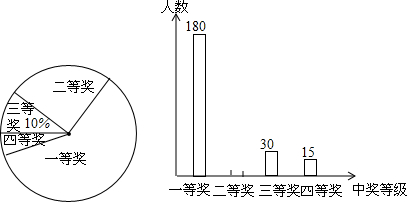
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
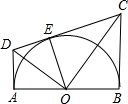 ��ͼ��ABΪ��ԲO��ֱ����AD��BC�ֱ��С�O��A��B���㣬CD�С�O�ڵ�E��AD��CD�ཻ��D��BC��CD�ཻ��C������OD��OE��OC���������н��ۣ�
��ͼ��ABΪ��ԲO��ֱ����AD��BC�ֱ��С�O��A��B���㣬CD�С�O�ڵ�E��AD��CD�ཻ��D��BC��CD�ཻ��C������OD��OE��OC���������н��ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
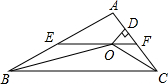 ��ͼ���ڡ�ABC�У���ABC�͡�ACB��ƽ�����ཻ�ڵ�O������O��EF��BC��AB��E����AC��F������O��OD��AC��D�������ĸ����ۣ��١�BOC=90��+$\frac{1}{2}$��A�� ��EF=BE+CF������OD=m��AE+AF=n����S��AEF=$\frac{1}{2}$mn�� ��EF�ǡ�ABC����λ�ߣ�������ȷ�Ľ����Ǣ٢ڢۣ�
��ͼ���ڡ�ABC�У���ABC�͡�ACB��ƽ�����ཻ�ڵ�O������O��EF��BC��AB��E����AC��F������O��OD��AC��D�������ĸ����ۣ��١�BOC=90��+$\frac{1}{2}$��A�� ��EF=BE+CF������OD=m��AE+AF=n����S��AEF=$\frac{1}{2}$mn�� ��EF�ǡ�ABC����λ�ߣ�������ȷ�Ľ����Ǣ٢ڢۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com