
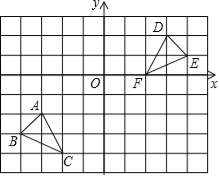
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC����DEF�Ķ��㶼�ڸ���ϣ����������ƽ��ֱ������ϵ����������⣺
��1��������ABC����ƽ��4����λ���Ⱥ����õ�����A1B1C1��
��2��������DEF�Ƶ�O��˳ʱ�뷽����ת90�������õ�����D1E1F1��
��3����A1B1C1����D1E1F1��ɵ�ͼ������Գ�ͼ��������ǣ���ֱ��д���Գ�������ֱ�ߵĽ���ʽ��
���𰸡���1����ͼ����������2����ͼ����������3���ǣ�y=x��
��������
���⣨1������ƽ�Ʊ任�������ı仯������������ȷ������A1��B1��C1λ��˳�����Ӽ��ɣ�
��2��������ת��������������ȷ������D1��E1��F1λ��˳�����Ӽ��ɣ�
��3��������Գ�ͼ�εĸ���ȷ���Գ��ᣬȻ������Գ�������ֱ�ߵĽ���ʽ��
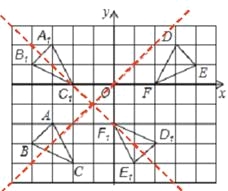
�����������1������ͼ����2������ͼ����A1B1C1����D1E1F1��ɵ�ͼ������Գ�ͼ�Σ��Գ���Ϊֱ��y=x��ֱ��y=-x-2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
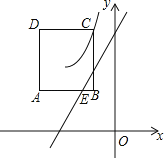
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳�Ϊ2��������ABCDλ�ڵڶ����ޣ���AB��x�ᣬ��B�ڵ�C�����·���˫����y��![]() ��x��0��������C��
��x��0��������C��
��1��m��ȡֵ��Χ���� ����
��2������B����1��1�����ж�˫�����Ƿ���A��
��3�����B��a��2a+1����
����˫���߾�����A����a��ֵ��
����ֱ��y��2x+2��AB�ڵ�E��˫�������߶�AE�н��㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��CD��BE�ֱ��ǡ�ABC�Ľ�ƽ���ߣ�AG��BC��AG��BG�����н��ۣ��١�BAG��2��ABF����BAƽ�֡�CBG���ۡ�ABG����ACB���ܡ�CFB��135����������ȷ�Ľ����У���������
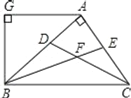
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����BC�ǡ�O�����ߣ�����AC���O���ڵ� D��ȡBC���е�E������DE��������OE����O�ڵ�F������AF��BC�ڵ�G������BD��AG�ڵ�H��
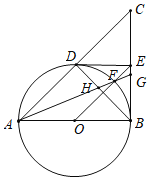
��1����EF��1��BE��![]() �����EOB�Ķ�����
�����EOB�Ķ�����
��2����֤��DEΪ��O�����ߣ�
��3����֤����FΪ�߶�HG���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����x2+bx+c����A��B���㣬��x�ύ����һ����C���Գ�����ֱ��AB���ڵ�E�������߶���ΪD��
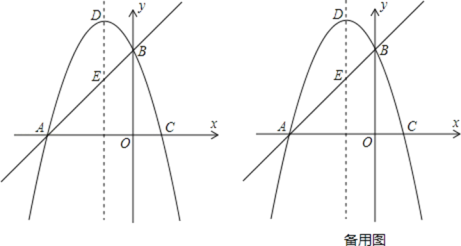
��1����A�������� ������B�������� ����
��2�����������ߵĽ���ʽ��
��ֱ��AB�������ߵĶԳ��ύ�ڵ�E����x�����Ƿ���ڵ�M��ʹ��ME+MB��С�������M�����꣮
��3����P�ӵ�D�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������˶���ʱ��Ϊt�룬��tΪ��ֵʱ����P��B��CΪ������������ǵ��������Σ�ֱ��д�����з���������tֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ե�����ABC��һ��ACΪֱ������O�����ױ�BC�ڵ�D������D����AB�Ĵ��ߣ�����ΪE����AC���ӳ����ڵ�F��
��1����֤��EF�ǡ�O�����ߣ�
��2��֤������CAD����CDF��
��3������F��30����AD��![]() �����O�������
�����O�������
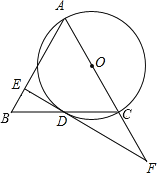
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��5��14����15������һ��һ·�����ʺ����߷���̳�ڱ������У�������̳�ڼ䣬�й�ͬ30��������ǩ��ó����Э�飬ij���������ס���������Ʒ��8����������һ��һ·�����߹��Һ͵�������֪2��������Ʒ��3��������Ʒ������������ͬ��3��������Ʒ��2��������Ʒ������������1500Ԫ.
(1)������Ʒ��������Ʒ�����۵��۸�����Ԫ��
(2)���ס���������Ʒ�����������벻����5400��Ԫ�����������ۼ�����Ʒ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c������A(��3��0)����C(0��3)����DΪ���κ����Ķ��㣬DEΪ���κ����ĶԳ��ᣬ��E��x���ϣ�
��1���������ߵĽ���ʽ������D�����ꣻ
��2����������A��C����֮����һ��F��ʹ��FAC����������F�����ꣻ
��3��ֱ��DE���Ƿ���ڵ�P��ֱ��AD�ľ����뵽x��ľ�����ȣ������ڣ��������P���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com