
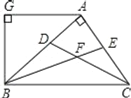
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个
A.1B.2C.3D.4
【答案】C
【解析】
由已知条件可知∠ABC+∠ACB=90°,又因为CD、BE分别是△ABC的角平分线,所以得到∠FBC+∠FCB=45°,所以求出∠CFB=135°;有平行线的性质可得到:∠ABG=∠ACB,∠BAG=2∠ABF.所以可知选项①③④正确.
∵AB⊥AC.
∴∠BAC=90°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=90°
∵CD、BE分别是△ABC的角平分线,
∴2∠FBC+2∠FCB=90°
∴∠FBC+∠FCB=45°
∴∠BFC=135°故④正确.
∵AG∥BC,
∴∠BAG=∠ABC
∵∠ABC=2∠ABF
∴∠BAG=2∠ABF 故①正确.
∵AB⊥AC,
∴∠ABC+∠ACB=90°,
∵AG⊥BG,
∴∠ABG+∠GAB=90°
∵∠BAG=∠ABC,
∴∠ABG=∠ACB 故③正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道数学中的整体思想吗?解题中,若把注意力和着眼点放在问题的整体上,多方位思考、联想、探究,进行整体思考、整体加减,能使问题迅速获解.
例题:已知x2+xy=4,xy+y2=-1.求代数式x2-y2的值.
解:将两式相减,得(x2+xy)-(xy+y2)=4-(-1),即x2-y2=5;请用整体思想解答下列问题:
(1)在例题的基础上求(x+y)2的值;
(2)若关于x、y的二元一次方程组![]() 的解也是二元一次方程x+y=6的解,求k的值.
的解也是二元一次方程x+y=6的解,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,点P在两平行线之间,点E. F分别在AB、CD上,连接PE,PF.尝试探究并解答:
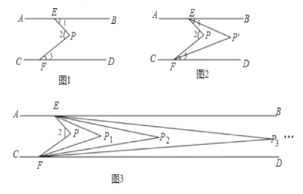
(1)若图1中∠1=36°,∠2=63°,则∠3=___;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2所示,∠1与∠3的平分线交于点P`,若∠2=α,试求∠EP`F的度数(用含α的代数式表示);
(4)如图3所示,在图2的基础上,若∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,∠BEP
,∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() …∠BEP
…∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,且∠2=α,直接写出∠EP
,且∠2=α,直接写出∠EP![]() F的度数(用含α的代数式表示).
F的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.

(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
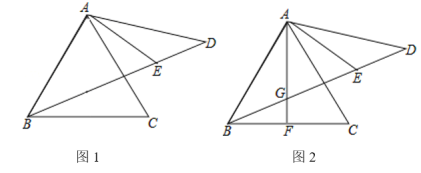
【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.

(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com