
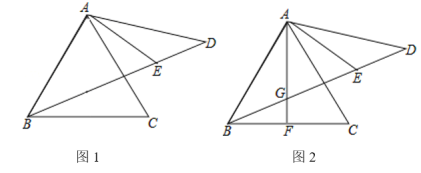
【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求![]() 的值.
的值.
【答案】(1)见解析;(2)60°;(3)![]()
【解析】
(1)利用等边三角形的性质可得AB=AC,又因为AD=AC已知,所以AB=AD,进而得到本题答案;
(2) 设∠3=∠D=x°,∠1=∠2=y°,利用等边三角形的性质以及三角形内角和定理得出∠3+∠D+∠BAD=180°,进而得出答案;
(3)首先得出△ABE≌△ADG ,进而得出∠4=∠AEB=60°,进而求出DE=BG=2GF, AG= BG=2GF, AF=AG+GF=3FG,即可得出答案.
解:(1)∵AB=AC,AD=AC,
∴AB=AD,
∴∠3=∠D(即∠ABD=∠D)
(2)∵AE平分∠CAD,
∴∠1=∠2,
∵△ABC是等边三角形,
∴∠BAC=60°,
设∠3=∠D=x°,∠1=∠2=y°,
∵∠3+∠D+∠BAD=180°,
∴x +x + 60° +2y =180°,
∴x +y =60°,
∴∠AEB=∠1+∠D = x +y = 60°;
(3)∵BG=DE,
∴BE=DG,
在△ABE和△ADG中,
![]()
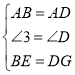 ,
,
∴△ABE≌△ADG(SAS)
∴∠4=∠AEB=60°
∵△ABC是等边三角形,F是BC中点,
∴∠AFB=90°,∠7=30°,
∵∠6=90°﹣∠5=30°,
∴DE=BG=2GF,
∵∠3=60°﹣∠6=30°=∠7,
∴AG=BG=2GF,
∴AF=AG+GF=3FG,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个
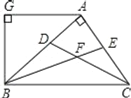
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 在数轴上表示的数分别是
在数轴上表示的数分别是![]() ,
,![]() ,将线段
,将线段![]() 分成
分成![]() 等分,离
等分,离![]() 点最近的分点为
点最近的分点为![]() ;再将线段
;再将线段![]() 分成
分成![]() 等份,其分点由左向右依次为
等份,其分点由左向右依次为![]() ;继续将线段
;继续将线段![]() 分成
分成![]() 等份,其分点由左向右依次为
等份,其分点由左向右依次为![]() ;
;![]() 对应的数用科学记数法表示为:________;
对应的数用科学记数法表示为:________;![]() 对应的数用科学记数法表示为:______.
对应的数用科学记数法表示为:______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉琪骑自行车从家去上学,当他以往常的速度骑了一段路后,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学过程中离家的路程(米)与所用时间(分钟)的关系示意图.根据图中提供的信息回答下列问题:

(1)嘉琪家到学校的距离是______米?书店到学校的距离是______米?
(2)本次上学途中嘉琪共行驶了_____米?本次嘉琪因为买书多走了______米的路?
(3)如果嘉琪不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?
(4)整个上学的途中在哪个时间段嘉琪骑车速度最快?最快的速度是多少米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com