
【题目】探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.

【答案】(1)110°;(2)60°
【解析】
(1)根据角平分线定理可知∠PBC+∠PCB =![]() ( ∠ABC+∠ACB ),∠A=40°已知,根据三角形内角和等于180°,可得∠ABC+∠ACB =140°,所以∠PBC+∠PCB =70°,再次根据三角形内角和可得∠P =110,即为答案.
( ∠ABC+∠ACB ),∠A=40°已知,根据三角形内角和等于180°,可得∠ABC+∠ACB =140°,所以∠PBC+∠PCB =70°,再次根据三角形内角和可得∠P =110,即为答案.
(2)根据BP、BQ三等分∠ABC,CP、CQ三等分∠ACB可得∠QBC+∠QCB=![]() ( ∠ABC+∠ACB )= 60°,所以∠BQC=120°,又由BP平分∠QBC, CP平分∠QCB,可得PQ平分∠BQC,所以∠BQP =
( ∠ABC+∠ACB )= 60°,所以∠BQC=120°,又由BP平分∠QBC, CP平分∠QCB,可得PQ平分∠BQC,所以∠BQP =![]() ×∠BQC =60° , 即得出答案.
×∠BQC =60° , 即得出答案.
解:(1)∵∠A+∠ABC+∠ACB = 180°
∴∠ABC+∠ACB=180° -∠A =140°
∵BP平分∠ABC, CP平分∠ACB
∴ ∠PBC+∠PCB=![]() ( ∠ABC+∠ACB )=70°
( ∠ABC+∠ACB )=70°
∵∠P+∠PBC+∠PCB = 180°
∴∠P=180°-(∠PBC+∠PCB)=110°
(2)∵∠A+∠ABC+ ∠ACB = 180°
∴∠ABC+∠ACB=180° -∠A =90°
∵BQ三等分∠ABC,CQ三等分∠ACB
∴ ∠QBC+∠QCB=![]() ( ∠ABC+∠ACB )=60°
( ∠ABC+∠ACB )=60°
∵∠Q+∠QBC+∠QCB= 180°
∴∠Q=180°-(∠QBC+∠QCB)=120°
∵BP平分∠QBC, CP平分∠QCB
∴PQ平分∠BQC
∴∠BQP =![]() ×120°=60°
×120°=60°


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
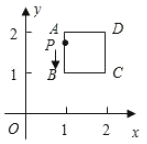
【题目】如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A. 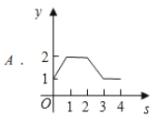 B.
B. 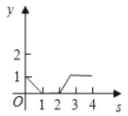 C.
C. 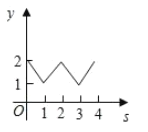 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,点P在两平行线之间,点E. F分别在AB、CD上,连接PE,PF.尝试探究并解答:
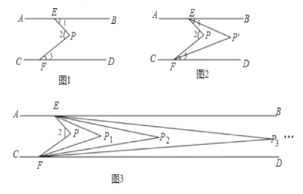
(1)若图1中∠1=36°,∠2=63°,则∠3=___;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2所示,∠1与∠3的平分线交于点P`,若∠2=α,试求∠EP`F的度数(用含α的代数式表示);
(4)如图3所示,在图2的基础上,若∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,∠BEP
,∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() …∠BEP
…∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,且∠2=α,直接写出∠EP
,且∠2=α,直接写出∠EP![]() F的度数(用含α的代数式表示).
F的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
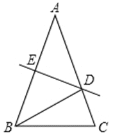
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB于E,交AC于D,连接BD.
(1)如果∠A=40°,求∠CBD的度数;
(2)若AB=AC=9cm,BC=5cm,求△BCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
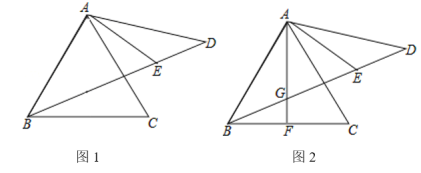
【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
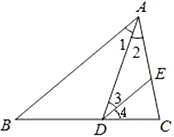
【题目】完成下面的推理填空
如图,已知![]() 是
是![]() 的角平分线,
的角平分线,![]() ,试证明:
,试证明:![]() .
.
证明:
![]() 是
是![]() 的角平分线(已知)
的角平分线(已知)
![]() ___________( )
___________( )
又![]() (已知)
(已知)
![]() ___________( )
___________( )
![]() ___________( )
___________( )
![]() ___________( )
___________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片的一角作折叠,使顶点 A 落在 A处, DE 为折痕,将 BEA对折,使得 B落在直线 EA上,得折痕 EG .
(1)求 DEG 的度数;
(2) 若 EA恰好平分 DEB ,求 DEA的度数 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com