
【题目】完成下面的推理填空
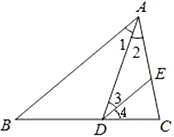
如图,已知![]() 是
是![]() 的角平分线,
的角平分线,![]() ,试证明:
,试证明:![]() .
.
证明:
![]() 是
是![]() 的角平分线(已知)
的角平分线(已知)
![]() ___________( )
___________( )
又![]() (已知)
(已知)
![]() ___________( )
___________( )
![]() ___________( )
___________( )
![]() ___________( )
___________( )
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________.
,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款386元,这两种商品原销售价之和为500元.问:这两种商品的原销售价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉琪骑自行车从家去上学,当他以往常的速度骑了一段路后,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学过程中离家的路程(米)与所用时间(分钟)的关系示意图.根据图中提供的信息回答下列问题:

(1)嘉琪家到学校的距离是______米?书店到学校的距离是______米?
(2)本次上学途中嘉琪共行驶了_____米?本次嘉琪因为买书多走了______米的路?
(3)如果嘉琪不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?
(4)整个上学的途中在哪个时间段嘉琪骑车速度最快?最快的速度是多少米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进4个红球和6个黑球.
(1)若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A. 若事件A为必然事件,则m= .
(2)若先从袋子里取出n个黑球,再放入2n个红球,若随机摸出一个球是红球的概率等于2/3,通过计算求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H.且点C是![]() 的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
的中点,若扇形的半径为3.则图中阴影部分的面积等于______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com