练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

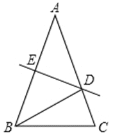
    【题目】如图，在△ABC中，AB＝AC，DE垂直平分AB于E，交AC于D，连接BD．

    （1）如果∠A＝40°，求∠CBD的度数；

    （2）若AB＝AC＝9cm，BC＝5cm，求△BCD的周长．

    【答案】（1）30°；（2）14cm

    【解析】

    (1)首先计算出∠ABC的度数，再根据线段垂直平分线上任意一点，到线段两端点的距离相等可得AD=BD，进而可得∠DBA=∠A=40°，然后可得答案;

    (2)根据线段垂直平分线的性质可得AD=DB,AE=BE,然后再计算出AC+ BC的长即为△ABC的周长，即可得答案.

    解：（1）∵AB=AC，∠A=40°

    ∴∠ABC＝∠C=70°

    ∵DE垂直平分AB

    ∴AD＝BD

    ∵∠DBA＝∠A＝40°

    ∴∠DBC＝70°－40°＝30°

    （2）∵由（1）DA＝DB已证

    ∴C△BCD＝BD+CD+BC＝AC +BC＝9+5＝14cm

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

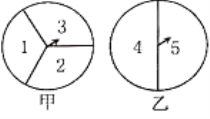
    【题目】如图，甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形．小夏和小秋利用它们来做决定获胜与否的游戏．规定小夏转甲盘一次、小秋转乙盘一次为一次游戏（当指针指在边界线上时视为无效，重转）.

    （1）小夏说：“如果两个指针所指区域内的数之和为6或7，则我获胜；否则你获胜”.按小夏设计的规则，请你写出两人获胜的可能性分别是多少?

    （2）请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则，并用一种合适的方法(例如：树状图，列表)说明其公平性.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系中的图形M和点P（点P在M内部或M上），给出如下定义：

    如果图形M上存在点Q，使得，那么称点P为图形M的和谐点．

    已知点，，，．

    （1）在点，，中，矩形的和谐点是_________________；

    （2）如果直线上存在矩形的和谐点P，求出点P的横坐标t的取值范围；

    （3）如果直线上存在矩形的和谐点E，F，使得线段上的所有点（含端点）都是矩形的和谐点，且，求出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“五一”期间，某商场搞优惠促销，决定由顾客抽奖确定折扣．某顾客购买甲、乙两种商品，分别抽到七折（按售价的70%销售）和九折（按售价的90%销售），共付款386元，这两种商品原销售价之和为500元．问：这两种商品的原销售价分别为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知是等边三角形，D是BC边上的一个动点点D不与B，C重合是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．

    如图1，求证：≌；

    请判断图1中四边形BCEF的形状，并说明理由；

    若D点在BC边的延长线上，如图2，其它条件不变，请问中结论还成立吗？如果成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究：

    （1）如图1，在△ABC中，∠A＝40°，△ABC的内角平分线交于点P，求∠P的度数；

    （2）如图2，在△ABC中，∠A＝90°，BP、BQ三等分∠ABC，CP、CQ三等分∠ACB，连结PQ，求∠BQP的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准，共支付两种垃圾处理费5000元，从去年元月起，收费标准上调为：可回收垃圾处理费30元/吨，不可回收垃圾处理费100元/吨．若该企业去年处理的这两种垃圾数量与前年相比没有变化，但调价后就要多支付处理费9000元．

    （1）该企业前年处理的可回收垃圾和不可回收垃圾各多少吨？

    （2）该企业计划今年将上述两种垃圾处理总量减少到200吨，且可回收垃圾不少于不可回收垃圾处理量的3倍，则今年该企业至少有多少吨可回收垃圾？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线相交于点平分.

    （1）若，求的度数；（2）若，求的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于点H，连接OH，∠CAD=35°，则∠HOB的度数为______．

    查看答案和解析>>

    同步练习册答案