练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点、在数轴上表示的数分别是，，将线段分成等分，离点最近的分点为；再将线段分成等份，其分点由左向右依次为；继续将线段分成等份，其分点由左向右依次为；对应的数用科学记数法表示为：________；对应的数用科学记数法表示为：______．

    【答案】

    【解析】

    由题意得点B表示的数是0.1×，N1表示的数是0.1××，P1表示的数是0.1×××，进而表示出点P17，然后利用科学计数法表示出即可.

    ∵点、在数轴上表示的数分别是，，将线段分成等分，

    ∴OB=OA×=0.1×=0.01=10-2，

    ∵将线段分成等份，

    ∴ON1=OB×=0.01×=0.0001.

    ∵将线段分成等份，

    ∴OP1=ON1×=0.0001×=0.000001，

    ∴P17对应的数是0.000001×17=0.000017=1.7×10-5.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又剩下一个四边形，称为第二次操作；…依此类推，若第n次操作后，余下的四边形是菱形，则称原平行四边形为n阶准菱形，例如：如图1，ABCD中，若AB=1，BC=2，则ABCD为1阶准菱形．

    （1）理解与判断：

    邻边长分别为1和3的平行四边形是　 　阶准菱形；

    邻边长分别为3和4的平行四边形是　 　阶准菱形；

    （2）操作、探究与计算：

    ①已知ABCD的邻边长分别为2，a（a＞2），且是3阶准菱形，请画出ABCD及裁剪线的示意图，并在图形下方写出a的值；

    ②已知ABCD的邻边长分别为a，b（a＞b），满足a=7b+r，b=4r，请写出ABCD是几阶准菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝ax2－2ax＋c与y轴交于C点，与x轴交于A、B两点，点A的坐标是（-1,0），O是坐标原点，且OC=3OA．

    （1）求抛物线的函数表达式；

    （2）直接写出直线BC的函数表达式；

    （3）如图1，D为y轴的负半轴上的一点，且OD=2，以OD为边作正方形ODEF．将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动，在运动过程中，设正方形ODEF与△OBC重叠部分的面积为s，运动的时间为t秒（0＜t≤2）．

    求：①s与t之间的函数关系式；

    ②在运动过程中，s是否存在最大值？如果存在，直接写出这个最大值；如果不存在，请说明理由．

    （4）如图2，点P（1，k）在直线BC上，点M在x轴上，点N在抛物线上，是否存在以A、M、N、P为顶点的平行四边形？若存在，请直接写出M点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ACB＝90°，CD⊥AB，垂足为D，则下面的结论中正确的是（　　）

    ①BC与AC互相垂直；②AC与CD互相垂直；③点A到BC的垂线段是线段BC；④点C到AB的垂线段是线段CD；③线段BC是点B到AC的距离；⑥线段AC的长度是点A到BC的距离．

    A.①④③⑥B.①④⑥C.②③D.①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

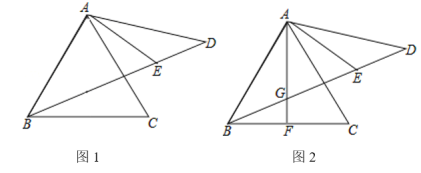
    【题目】如图1，D是等边△ABC外一点，且AD＝AC，连接BD，∠CAD的角平分交BD于E．

    （1）求证：∠ABD＝∠D；

    （2）求∠AEB的度数；

    （3）△ABC 的中线AF交BD于G（如图2），若BG＝DE，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对

    他们进行了六次测试，测试成绩如下表（单位：环）：


    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    甲

    10

    8

    9

    8

    10

    9

    乙

    10

    7

    10

    10

    9

    8

    （1）根据表格中的数据，计算出甲的平均成绩是 环，乙的平均成绩是 环；

    （2）分别计算甲、乙六次测试成绩的方差；

    （3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．

    （计算方差的公式：s2＝［］）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD的顶点坐标为A（—5，1），B（—1，1）， C（—1，6），D（—5，4），请作出四边形ABCD关于x轴及y轴的对称图形，并写出坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次知识竞赛中，甲、乙两人进入了“必答题”环节．规则是：两人轮流答题，每人都要回答20个题，每个题回答正确得a分，回答错误或放弃回答扣b分．当甲、乙两人恰好都答完12个题时，甲答对了8个题，得分为64分；乙答对了9个题，得分为78分．

    （1）求a和b的值；

    （2）规定此环节得分不低于120分能晋级，甲在剩下的比赛中至少还要答对多少个题才能顺利晋级？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠1+∠2＝180°，∠DAE＝∠BCF，DA平分∠BDF．

    （1）AD与BC的位置关系如何？为什么？

    （2）证明BC平分∠DBE．

    查看答案和解析>>

    同步练习册答案