
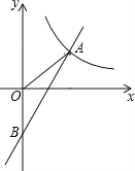
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
【答案】(1)![]() ,
,![]() ;(2)点C的坐标为
;(2)点C的坐标为![]() 或
或![]() ;(3)27.
;(3)27.
【解析】试题分析:(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出a值,从而得出反比例函数解析式;由勾股定理得出OA的长度从而得出点B的坐标,由点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,根据三角形的面积公式结合△ABC的面积是8,可得出关于m的含绝对值符号的一元一次方程,解方程即可得出m值,从而得出点C的坐标;
(3)设点E的横坐标为1,点F的横坐标为6,点M、N分别对应点E、F,根据反比例函数解析式以及平移的性质找出点E、F、M、N的坐标,根据EM∥FN,且EM=FN,可得出四边形EMNF为平行四边形,再根据平行四边形的面积公式求出平行四边形EMNF的面积S,根据平移的性质即可得出C1平移至C2处所扫过的面积正好为S.
试题解析:
(1)∵点A(4,3)在反比例函数y=![]() 的图象上,
的图象上,
∴a=4×3=12,
∴反比例函数解析式为y=![]() ;
;
∵OA=![]() =5,OA=OB,点B在y轴负半轴上,
=5,OA=OB,点B在y轴负半轴上,
∴点B(0,﹣5).
把点A(4,3)、B(0,﹣5)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=2x﹣5.
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,如图1所示.

令y=2x﹣5中y=0,则x=![]() ,
,
∴D(![]() ,0),
,0),
∴S△ABC=![]() CD(yA﹣yB)=
CD(yA﹣yB)=![]() |m﹣
|m﹣![]() |×[3﹣(﹣5)]=8,
|×[3﹣(﹣5)]=8,
解得:m=![]() 或m=
或m=![]() .
.
故当△ABC的面积是8时,点C的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
(3)设点E的横坐标为1,点F的横坐标为6,点M、N分别对应点E、F,如图2所示.

令y=![]() 中x=1,则y=12,
中x=1,则y=12,
∴E(1,12),;
令y=![]() 中x=4,则y=3,
中x=4,则y=3,
∴F(4,3),
∵EM∥FN,且EM=FN,
∴四边形EMNF为平行四边形,
∴S=EM(yE﹣yF)=3×(12﹣3)=27.
C1平移至C2处所扫过的面积正好为平行四边形EMNF的面积.
故答案为:27.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】小明想要做以下的一个探究:小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干. 先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.由此可知A型号与B型号钢球的体积比为____________;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?

查看答案和解析>>
科目:初中数学 来源: 题型:
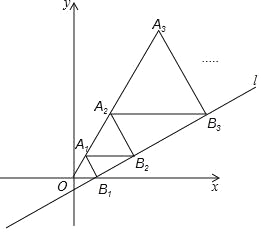
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(0,1),B(5,0)将线段AB向上平移到DC,如图1,CD交y轴于点E,D点坐标为(﹣2,a)
(1)直接写出点C坐标(C的纵坐标用a表示);
(2)若四边形ABCD的面积为18,求a的值;
(3)如图2,F为AE延长线上一点,H为OB延长线上一点,EP平分∠CEF,BP平分∠ABH,求∠EPB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是( )

A. ①② B. ①②④ C. ③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
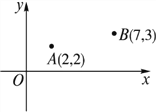
【题目】A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7, 3),根据下列要求作图(保留作图痕迹,不用写作法).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点;
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,P点的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
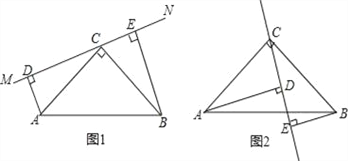
【题目】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.求证:
(1)△ADC≌△CEB;
(2)DE=AD+BE.
(3)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
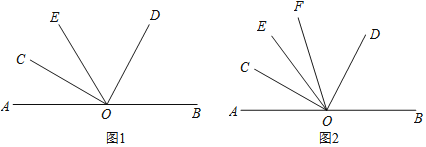
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com