
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
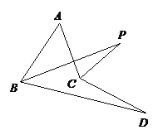
A.15°B.20°C.25°D.30°
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图将矩形ABCD的四个内角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )

A. 8+6![]() B. 12
B. 12![]() C. 19.2D. 20
C. 19.2D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种股票第一天的最高价比开盘价高0.3元,最低价比开盘价低0.2元;第二天的最高价开盘价高0.2元,最低价比开盘价低0.1元;第三天的最高价等于开盘价,最低价比开盘价低0.13元.计算每天最高价与最低价的差,以及这些差的平均值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
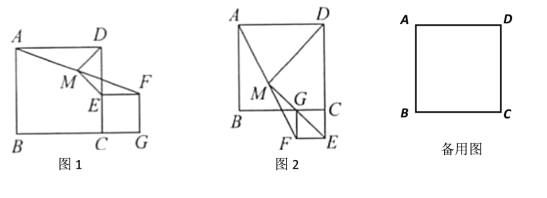
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
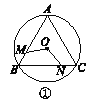
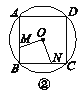
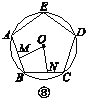
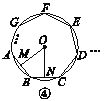
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=![]() AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
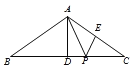
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC=___________。
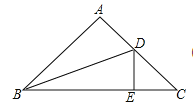
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com