
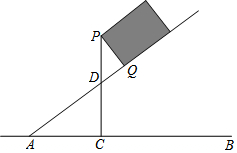
 一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.
一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC. 分析 根据正切的定义求出DQ,根据勾股定理求出PD,根据相似三角形的性质居计算即可.
解答 解:由题意得,∠DPQ=α,
∴tan∠DPQ=$\frac{3}{4}$,即$\frac{DQ}{PQ}$=$\frac{3}{4}$,
∴DQ=$\frac{3}{4}$h,
∴PD=$\sqrt{P{Q}^{2}+D{Q}^{2}}$=$\frac{5}{4}$h,AQ=m-$\frac{3}{4}$h,
∵△ACD∽△PQD,
∴$\frac{CD}{DQ}$=$\frac{AD}{PD}$,即$\frac{CD}{\frac{3}{4}h}$=$\frac{m-\frac{3}{4}h}{\frac{5}{4}h}$,
解得,CD=$\frac{3}{5}$m-$\frac{9}{20}$h,
∴PC=CD+PD=$\frac{3}{5}$m+$\frac{4}{5}$h.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$(x-1)2-$\frac{1}{2}$ | B. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2+$\frac{1}{32}$ | C. | y=$\frac{1}{2}$(x-1)2+$\frac{1}{2}$ | D. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2-$\frac{1}{32}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
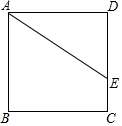 已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.
已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
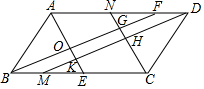 如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形.
如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 0 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com