
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
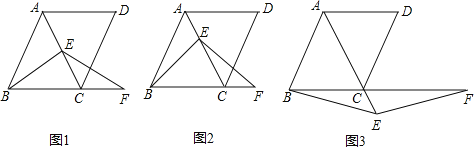
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
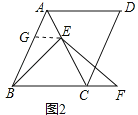
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)△ABC的面积=![]() ;(2)见解析;(3)成立,证明见解析.
;(2)见解析;(3)成立,证明见解析.
【解析】
试题分析:(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
解:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=![]() AB=1,
AB=1,
∴BE=![]() ,
,
∴△ABC的面积=![]() ×AC×BE=
×AC×BE=![]() ;
;
(2)如图2,作EG∥BC交AB于G,
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
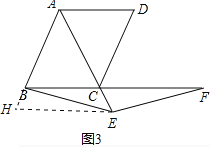
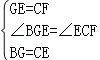 ,
,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,
如图3,作EH∥BC交AB的延长线于H,
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
 ,
,
∴△BHE≌△ECF,
∴EB=EF.


科目:初中数学 来源: 题型:
【题目】下列三角形一定不是直角三角形的是( )
A. 三角形的三边长分别为5,12,13 B. 三角形的三个内角比为1:2:3
C. 其中有两个角互余 D. 三边长的平方比为3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
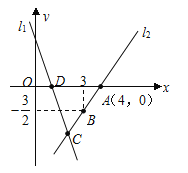
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求![]() 的面积;
的面积;
(4)在直线![]() 上存在异于点
上存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+a,下列说法中正确的是 (填写序号).
①当x<0时,y随x的增大而减小;
②若图象与x轴有交点,则a≤4;
③若将图象向上平移1个单位长度,再向左平移3个单位长度后过点(1,﹣2),则a=﹣3;
④当a=3时,不等式x2﹣4x+a>0的解集是1<x<3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
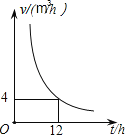
①请你根据图象提供的信息求出此蓄水池的蓄水量;
②写出此函数的解析式;
③若要6h排完水池中的水,那么每小时的排水量应该是多少?
④如果每小时排水量是5m3,那么水池中的水将要多少小时排完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点P关于x轴的对称点在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
A.(﹣3,﹣2) B.(﹣2,﹣3) C.(2,3) D.(3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点 T ( m , n )表示火炬位置,火炬从离北京路10 m 处的 M 点开始传递,到离北京路1 000 m 的 N 点时传递活动结束.迎圣火临时指挥部设在坐标原点 O (北京路与奥运路的十字路口), OATB 为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000 m 2 .(路线宽度均不计)
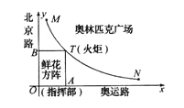
(1)、求图中反比例函数的关系式(不需写出自变量的取值范围);
(2)、当鲜花方阵的周长为500 m 时,确定此时火炬的位置(用坐标表示);
(3)、设t=m-n ,用含 t 的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com