
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
【答案】(1)y=﹣0.5x+160(120≤x≤180);(2)当销售单价为180元时,销售利润最大,最大利润是7000元.
【解析】试题分析:(1)首先由表格可知:销售单价没涨10元,就少销售5kg,即可得y与x是一次函数关系,则可求得答案;
(2)首先设销售利润为w元,根据题意可得二次函数,然后求最值即可.
试题解析:(1)∵由表格可知:销售单价没涨10元,就少销售5kg,∴y与x是一次函数关系,∴y与x的函数关系式为:y=100﹣0.5(x﹣120)=﹣0.5x+160,∵销售单价不低于120元/kg.且不高于180元/kg,∴自变量x的取值范围为:120≤x≤180;
(2)设销售利润为w元,则w=(x﹣80)(﹣0.5x+160)=![]() ,∵a=
,∵a=![]() <0,∴当x<200时,y随x的增大而增大,∴当x=180时,销售利润最大,最大利润是:w=
<0,∴当x<200时,y随x的增大而增大,∴当x=180时,销售利润最大,最大利润是:w=![]() =7000(元).
=7000(元).
答:当销售单价为180元时,销售利润最大,最大利润是7000元.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
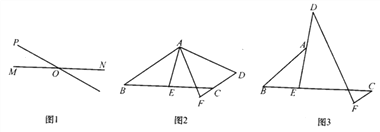
【题目】(l)操作:如图1,点O为线段MN的中点,直线PQ与MN相交于点O,请利用图1画出一对以点O为对称中心的全等三角形;根据上述操作得到的经验完成下列探究活动:
(2)探究一:如图2,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.试探究线段AB与AF,AF,CF之间的等量关系,并证明你的结论;
(3)探究二:如图3 ,DE,BC相交于点E,BA交DE于点A,且BE:EC=1:2,∠BAE=∠EDF,CF∥AB.若AB=5,CF=1,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路边有一灯杆AB,在A点灯光的照耀下,点D处一直立标杆CD的影子为DH,沿BD方向的F处有另一标杆EF,其影子为FG,
(1)在图中画出灯杆AB,并标上相应的字母;(不写画法,保留画图痕迹)
(2)已知标杆EF=1.6m,影长FG=4m,灯杆AB到标杆EF的距离BF=8m,求灯杆AB的长.
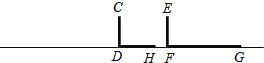
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的含![]() 角的直角三角板按图
角的直角三角板按图![]() 的方式放置,已知
的方式放置,已知![]() ,
,![]() .
.
![]() 固定三角板
固定三角板![]() ,然后将三角板
,然后将三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
①填空:当旋转角等于![]() 时,
时,![]() ________度;
________度;
②当旋转角等于多少度时,![]() 与
与![]() 垂直?请说明理由.
垂直?请说明理由.
![]() 将图
将图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,使
所示的位置,使![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试说明
,试说明![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
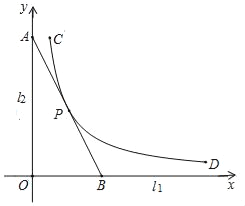
【题目】如图,直线l1,l2是紧靠某湖泊的两条相互垂直的公路,曲线段CD是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路AB,用以连接两条公路和环湖观光大道,且直线AB与曲线段CD有且仅有一个公共点P.已知点C到l1,l2的距离分别为8km和1km,点P到l1的距离为4km,点D到l1的距离为0.8km.若分别以l1,l2为x轴、y轴建立平面直角坐标系xOy,则曲线段CD对应的函数解析式为y=![]() .
.
(1)求k的值,并指出函数y=![]() 的自变量的取值范围;
的自变量的取值范围;
(2)求直线AB的解析式,并求出公路AB长度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com