
【题目】将两块全等的含![]() 角的直角三角板按图
角的直角三角板按图![]() 的方式放置,已知
的方式放置,已知![]() ,
,![]() .
.
![]() 固定三角板
固定三角板![]() ,然后将三角板
,然后将三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
①填空:当旋转角等于![]() 时,
时,![]() ________度;
________度;
②当旋转角等于多少度时,![]() 与
与![]() 垂直?请说明理由.
垂直?请说明理由.
![]() 将图
将图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,使
所示的位置,使![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试说明
,试说明![]() .
.

【答案】(1)①![]() ;②当旋转角等于
;②当旋转角等于![]() 时,
时,![]() 与
与![]() 垂直,理由详见解析;(2)详见解析.
垂直,理由详见解析;(2)详见解析.
【解析】
(1)①根据旋转的性质得∠A1CA=20°,则利用互余得∠ACB1=70°,然后根据∠BCB1=∠ACB+∠ACB1进行计算;
②利用AB与A1B1垂直得∠A1ED=90°,则∠A1DE=90°-∠A1=60°,根据对顶角相等得∠BDC=60°,由于∠B=60°,利用三角形内角和定理得∠A1CB=180°-∠BDC-∠B=60°,所以∠ACA1=90°-∠A1CB=30°,然后根据旋转的定义得到旋转角等于30°时,AB与A1B1垂直;
(2)由于AB∥CB1,∠ACB1=90°,根据平行线的性质得∠ADC=90°,在Rt△ADC中,根据含30度的直角三角形三边的关系得到CD=![]() AC,再根据旋转的性质得AC=A1C,所以CD=
AC,再根据旋转的性质得AC=A1C,所以CD=![]() A1C,则A1D=CD.
A1C,则A1D=CD.
(1)①∵将三角板ABC绕点C顺时针方向旋转至图2所示的位置,
∴∠A1CA=20°
∴∠ACB1=70°,
∴∠BCB1=∠ACB+∠ACB1=160°;
故答案为160;
②当旋转角等于![]() 时,
时,![]() 与
与![]() 垂直.理由如下:
垂直.理由如下:
当![]() 与
与![]() 垂直时,
垂直时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
即旋转角等于![]() 时,
时,![]() 与
与![]() 垂直;
垂直;
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
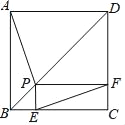
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
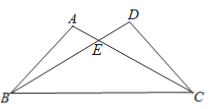
【题目】如图,已知∠A=∠D有下列五个条件①AE=DE ②BE=CE ③AB=DC ④∠ABC=∠DCB⑤AC=BD能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康.你知道吗,被动吸烟也大大危害着人类的健康.为此,联合国规定每年的5月31日为世界无烟日.为配合今年的“世界无烟日”宣传活动,小明和同学们在学校所在地区展开了以“我支持的戒烟方式”为主题的问卷调查活动,征求市民的意见,并将调查结果分析整理后,制成下列统计图:

(1)求小明和同学们一共随机调查了多少人?
(2)根据以上信息,请你把统计图补充完整;
(3)如果该地区有2万人,那么请你根据以上调查结果,估计该地区大约有多少人支持“强制戒烟”这种戒烟方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将推理过程填写完整
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。求∠AGD的度数。
解:因为EF∥AD(已知)
所以 ∠2 = (两直线平行,同位角相等)
又因为 ∠1 = ∠2(已知)
所以 ∠1 = ∠3(等量代换)
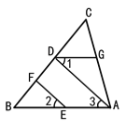
所以AB∥ ( )
所以∠BAC + = 180°( )
又因为∠BAC = 70°(已知)
所以∠AGD =
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)小明解不等式![]() ≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
解:去分母得:3(1+x)﹣2(2x+1)≤1……①
去括号得:3+3x﹣4x+1≤1……②
移项得:3x﹣4x≤1﹣3﹣1……③
合并同类项得:﹣x≤﹣3……④
两边都除以﹣1得:x≤3……⑤
解:开始出现错误的步骤序号为 ,正确的解答过程 .
(3)已知实数x,y满足方程组![]() ,求
,求![]() 的平方根;
的平方根;
(4)求不等式组 的整数解.
的整数解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com