
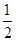 x2+20x��0��x��15����
x2+20x��0��x��15����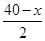 ���������ʽ��ʾ���������
���������ʽ��ʾ��������� ��
��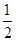 x2+20x��0��x��15����
x2+20x��0��x��15����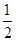 x2+20x=200��
x2+20x=200��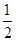 x2+20x��ͼ���ǿ������µ������ߣ��Գ���Ϊx=20��
x2+20x��ͼ���ǿ������µ������ߣ��Գ���Ϊx=20��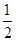 ��152+20��15=187.5m2
��152+20��15=187.5m2

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��y�ύ�ڣ�0,3����
��y�ύ�ڣ�0,3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
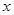 Ԫ��ÿ�۳�һ��С�ҵ�ɻ�õ������Ƕ���Ԫ�����ú�
Ԫ��ÿ�۳�һ��С�ҵ�ɻ�õ������Ƕ���Ԫ�����ú�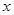 �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��ö��κ�������A,B����,����A�㣨3,4��,B����y����.
��ö��κ�������A,B����,����A�㣨3,4��,B����y����.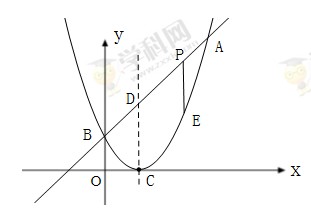
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮
���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ���������������ε�����ĺ�S����
���������������ε�����ĺ�S���� �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪA��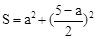 | B��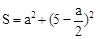 |
C��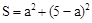 | D��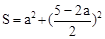 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

| A��a��0 | B��3�Ƿ���ax²+bx+c=0��һ���� |
| C��a+b+c=0 | D����x��1ʱ��y��x���������С |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com