
【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
【答案】(1)m>﹣![]() .(2)当m=﹣1时,此方程的根为x1=﹣1和x2=﹣2.
.(2)当m=﹣1时,此方程的根为x1=﹣1和x2=﹣2.
【解析】
试题分析:(1)由方程有两个不等实数根可得b2﹣4ac>0,代入数据即可得出关于m的一元一次不等式,解不等式即可得出结论;
(2)根据m为负整数以及(1)的结论可得出m的值,将其代入原方程,利用分解因式法解方程即可得出结论.
试题解析:(1)∵关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根,
∴△=b2﹣4ac=32﹣4(1﹣m)>0,
即5+4m>0,解得:m>﹣![]() .
.
∴m的取值范围为m>﹣![]() .
.
(2)∵m为负整数,且m>﹣![]() ,∴m=﹣1.
,∴m=﹣1.
将m=﹣1代入原方程得:x2+3x+2=(x+10)(x+2)=0,
解得:x1=﹣1,x2=﹣2.
故当m=﹣1时,此方程的根为x1=﹣1和x2=﹣2.


科目:初中数学 来源: 题型:
【题目】在一次食品安检中,抽查某企业10袋奶粉,每袋取出100克,检测每100克奶粉蛋白质含量与规定每100克含量(蛋白质)比较,不足为负,超过为正,记录如下:(注:规定每100g奶粉蛋白质含量为15g)
﹣3,﹣4,﹣5,+1,+3,+2,0,﹣1.5,+1,+2.5
(1)求平均每100克奶粉含蛋白质为多少?
(2)每100克奶粉含蛋白质不少于14克为合格,求合格率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )

A. 甲的速度随时间的增加而增大
B. 乙的平均速度比甲的平均速度大
C. 在起跑后第180秒时,两人相遇
D. 在起跑后第50秒时,乙在甲的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
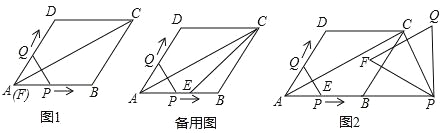
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙在400米的直线跑道上从同一地点同向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,跑步过程中两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
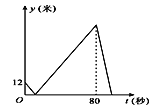
A. 乙的速度是4米/秒
B. 离开起点后,甲、乙两人第一次相遇时,距离起点12米
C. 甲从起点到终点共用时83秒
D. 乙到达终点时,甲、乙两人相距68米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com