Question

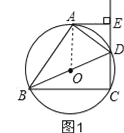
【题目】如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作AE⊥CD，交CD的延长线于点E，DA平分∠BDE．

（1）求证：AE是⊙O的切线；

（2）已知AE=4cm，CD=6cm，求⊙O的半径．

Answer 1

【答案】(1)证明见解析

【解析】

试题分析：（1）连接OA，因为点A在⊙O上，所以只要证明OA⊥AE即可；由同圆的半径相等得：OA=OD，则∠ODA=∠OAD，根据角平分线可知：∠OAD=∠EDA，所以EC∥OA，由此得OA⊥AE，则AE是⊙O的切线；

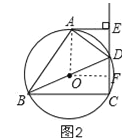
（2）过点O作OF⊥CD，垂足为点F，证明四边形AOFE是矩形，得OF=AE=4cm，由垂径定理得：DF=3，根据勾股定理求半径OD的长．

试题解析：（1）连结OA，∵OA=OD，∴∠ODA=∠OAD，∵DA平分∠BDE，

∴∠ODA=∠EDA，∴∠OAD=∠EDA，∴EC∥OA，

∵AE⊥CD，∴OA⊥AE，

∵点A在⊙O上，

∴AE是⊙O的切线；

（2）过点O作OF⊥CD，垂足为点F，∵∠OAE=∠AED=∠OFD=90°，∴四边形AOFE是矩形，∴OF=AE=4cm，

又∵OF⊥CD，∴DF=CD=3cm，在Rt△ODF中，OD==5cm，

即⊙O的半径为5cm．