练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，△ABC的顶点都在格点上，点B的坐标是（1，2）．

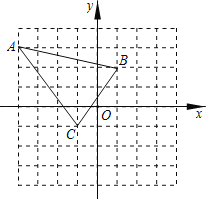
    （1）将△ABC先向右平移3个单位长度，再向下平移2个单位长度，得到△A'B'C'．请画出△A'B'C'并写出A'，B′，C'的坐标；

    （2）在△ABC内有一点P（a，b），请写出按（1）中平移后的对应点P″的坐标．

    【答案】（1）图见解析，点A'，B′，C'的坐标分别为（﹣1，1），（4，0），（2，﹣3）；（2）（a+3，b﹣2）

    【解析】

    （1）利用点平移的坐标变换规律写出A'，B′，C'的坐标，然后描点即可；

    （2）利用（1）中的平移规律，把P点的横坐标加3，纵坐标减2得到P′点的坐标．

    解：（1）如图，△A'B'C'为所作，点A'，B′，C'的坐标分别为（﹣1，1），（4，0），（2，﹣3）；

    （2）点P（a，b）平移后的对应点P″的坐标为（a+3，b﹣2）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

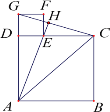
    【题目】如图，已知四边形和四边形为正方形，点在线段上，点在同一直线上，连接，并延长交于点．

    （1）求证：．

    （2）若，，求线段的长．

    （3）设，，当点H是线段GC的中点时，则与满足什么样的关系式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

    （1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

    （2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

    （3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

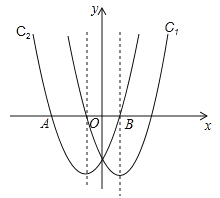
    【题目】在同一直角坐标系中，抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．

    （1）求抛物线C1，C2的函数表达式；

    （2）求A、B两点的坐标；

    （3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

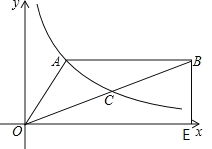
    【题目】如图，双曲线y=（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），BE⊥x轴，垂足为E．

    （1）确定k的值；

    （2）若点D（3，m）在双曲线上，求直线AD的解析式；

    （3）计算△OAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

    （1）求证：AD=AF；

    （2）如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

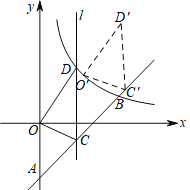
    【题目】如图，一次函数y＝kx－4（k≠0）的图象与y轴交于点A，与反比例函数y＝（x＞0）的图象交于点B（6，b）．

    （1）b＝__________；k＝__________．

    （2）点C是直线AB上的动点（与点A，B不重合），过点C且平行于y轴的直线l交这个反比例函数的图象于点D，当点C的横坐标为3时，得△OCD，现将△OCD沿射线AB方向平移一定的距离（如图），得到△O′C′D′，若点O的对应点O′落在该反比例函数图象上，求点O′，D′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

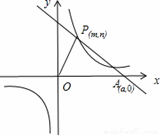
    【题目】已知：O是坐标原点，P（m，n）(m＞0)是函数y ＝ (k＞0)上的点，过点P作直线PA⊥OP于P，直线PA与x轴的正半轴交于点A（a，0）(a＞m). 设△OPA的面积为s，且s＝1＋.

    （1）当n＝1时，求点A的坐标；

    （2）若OP＝AP，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了了解初中各年级学生每天的平均睡眠时间（单位：h，精确到1 h），抽样调查了部分学生，并用得到的数据绘制了下面两幅不完整的统计图．

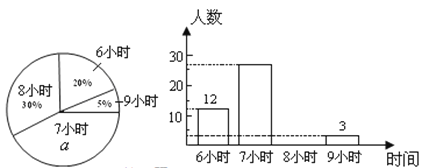
    请你根据图中提供的信息，回答下列问题：

    （1）求出扇形统计图中百分数的值为_______，所抽查的学生人数为______；

    （2）求出平均睡眠时间为8小时的人数，并补全条形图；

    （3）求出这部分学生的平均睡眠时间的平均数；

    （4）如果该校共有学生1200名，请你估计睡眠不足（少于8小时）的学生数.

    查看答案和解析>>

    同步练习册答案