Question

【题目】如图，在8×8的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.

（1）在图中作出△ABC关于直线l对称的△A1B1C1；（要求：A与A1，B与B1，C与C1相对应）

（2）是 三角形；

（3）若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有 个；

(4)在直线上找一点Q，使QB+QC的值最小。

Answer 1

【答案】（1）答案见解析；（2）等腰直角；（3）4；（4）答案见解析.

【解析】

（1）分别作出点A、B、C关于直线l的对称点，再顺次连接可得；

（2）根据网格，求出AB，AC，BC的长度，然后再判断即可；

（3）作线段AB的垂直平分线，即可得到答案；

（4）连接，与相交于一点，这点为点Q，由垂直平分线性质，QC=，则得到QB+QC的最小值.

解：（1）如图所示：△A1B1C1为所求.

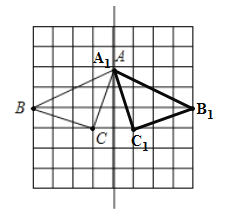
（2）根据题意，可知，

，，，

∴，

∵，

∴是等腰直角三角形；

故答案为：等腰直角.

（3）如图，作线段AB的垂直平分线，与网格的顶点相交即为点P；

由图可知，使PA=PB的点P一共有4个，

故答案为：4.

（4）如图，连接与相交于点Q，则QB+QC取到最小值；

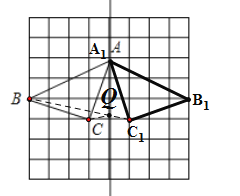
∵垂直平分，

∴，

∴QB+QC=QB+，

∴最小值为：；