
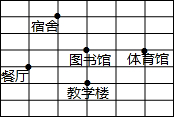
 下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可).
下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可). 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
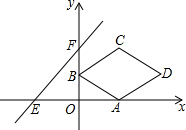 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
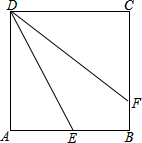 如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE.
如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE.查看答案和解析>>
科目:初中数学 来源: 题型:
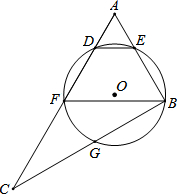 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
| ||
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
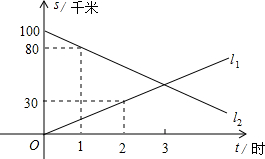 甲、乙两人骑车分别从A、B两地同时出发,相向而行,假设他们都保持匀速行驶,则甲、乙两人各自距A地的距离s(千米)与行驶的时间t(时)的关系分别用图中直线l1、l2在第一象限的部分表示.
甲、乙两人骑车分别从A、B两地同时出发,相向而行,假设他们都保持匀速行驶,则甲、乙两人各自距A地的距离s(千米)与行驶的时间t(时)的关系分别用图中直线l1、l2在第一象限的部分表示.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,⊙O是△ACD的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.∠BCF=30°.当∠DAC满足什么条件时,CF是⊙O的切线.请给予证明.
已知:如图,⊙O是△ACD的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.∠BCF=30°.当∠DAC满足什么条件时,CF是⊙O的切线.请给予证明.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com