
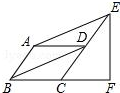
 如图,在平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD.
如图,在平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD.分析 (1)根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,进而可证明点D为CE的中点;
(2)根据直角三角形性质求出CE长,利用勾股定理即可求出AB的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC且AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,即D为CE中点;
(2)解:∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=$\sqrt{3}$,
∴CE=2,
∴AB=$\sqrt{C{E}^{2}-E{F}^{2}}$=1.
点评 本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.


科目:初中数学 来源: 题型:选择题
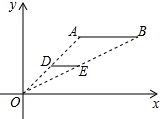 如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )
如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )| A. | (1,1) | B. | (1,2) | C. | (2,1) | D. | (2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.3×106 | B. | 1.3×107 | C. | 1.3×108 | D. | 1.3×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
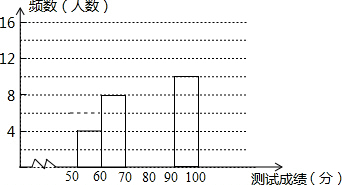 为了提高学生的环保意识,我校举办了“地球知识大赛”,经选拔后有50名学生参加决赛,这50名学生同时填写答卷,答卷共50题,若每答对1题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图表:
为了提高学生的环保意识,我校举办了“地球知识大赛”,经选拔后有50名学生参加决赛,这50名学生同时填写答卷,答卷共50题,若每答对1题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com