练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在函数y= 中，自变量x的取值范围是_________          



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


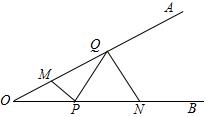
    如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


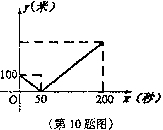
    甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点，甲在乙前面,若甲乙同时起跑至乙到达终点的过程中，甲乙之间的距离y(米)与时间t(秒)之间的函数 关系如图所示.有下列说法:①甲的速度为4米/秒;②50秒时 乙追上甲;③25秒时甲乙相距50米;④乙到达终点时甲 距终点400米.其中正确的说法有（ )•

    (A)l 个 (B) 2 个   (C)3 个 (D)4 个'

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，点0为坐标原点,抛物线y=-(x-2)(x-k)(k>2)与x轴交于点A、B(点 A在点B的左侧)，与y轴的负半轴交于点C，点D为抛物线的顶点，抛物线的对称轴交X轴于点E.

     (1)如图1，当AB=2时，求抛物线的解析式；

    (2)如图2，连接CD,过点0作CD的垂线,交抛物线y=-(x-2)(x-k)的对称轴于点F,求点 F的纵坐标；

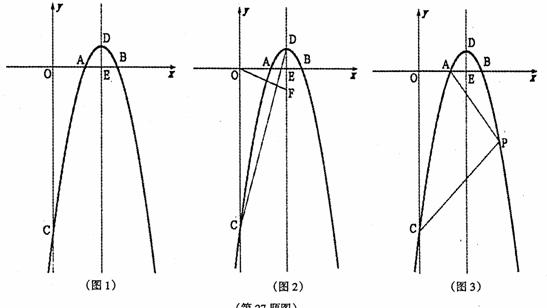    （3）在(1)的条件下，如图3，点P为在x轴下方,且在抛物线的对称轴右侧抛物线上的一动点，连接AP，当∠PAB=∠0CP时，求tan∠APB的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平行四边形ABCD中， E是BC延长线上一点, AE交CD 于F.且CE=BC，则（     ）

    A  B  C    D

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    随机掷一枚质地均匀的正方体锻子，骰子的六个面上分别刻有1到6的点数，则这个骰子向上的一面点数不大于4的概率为_____________   .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


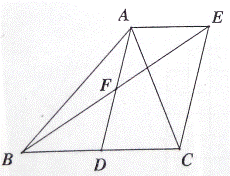
    如图,AD是△ ABC的中线，AE//BC，BE交AD于点F,且AF=DF.

    (1)求证：四边形ADCE是平行四边形；

    (2)当AB、AC之间满足_____________   时，四边形ADCE是矩形；

    (3)当AB、AC之间满足_____________时，四边形ADCE是正方形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC内接于⊙O，AO＝2，BC＝2，则∠BAC的度数为     °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    以下列长度的线段为边不能构成直角三角形的是（     ）

    A．3，4，5        B．6，8，10       C．5，12，13        D．6，24，25

    查看答案和解析>>

    同步练习册答案