
【题目】为了解学生自主学习的具体情况,童老师随机对部分学生进行了跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差,绘制成了以下两幅不完整的统计图(每位学生只属于一类),请你解答下列问题:

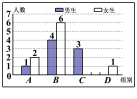
(1) 本次调查的样本容量为__________
(2) 将条形统计图补充完整
(3) D类所占扇形角的度数为__________
(4) 学校共有2000名学生,其中自主学习情况特别好的约有多少人?
【答案】(1)20;(2)补图见解析;(3)36°;(4)300名.
【解析】
(1)用A类(或B类)的男女生人数的和除以他们所占的百分比即可得到调查的总人数;
(2)先求出各类学生数,再补全条形统计图即可;
(3)用360°乘以D类所占的百分比即可得到圆心角的度数;
(4)用总人数2000乘以C、D类所占的百分比.
(1)10÷50%=20,
所以共调查了20名同学;
(2)20×25%=5,5-3=2,
所以C类女生有2名;
20-3-10-5=2,2-1=1,
所以D类男生有1名;
如图;

(3)D类所占比例为:1-15%-25%-50%=10%,
360°×10%=36°;
(3)2000×![]() =300(名),
=300(名),
答:估计该校自主学习情况特别好的学生约有300名.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,某小区有东西方向的街道3条,南北方向的街道4条,从位置A出发沿街道行走到达位置B,要求路程最短,研究有多少种不同的走法. 小聪是这样思考的:要使路程最短,就不能走“回头路”,只能分五步来完成,其中三步向右行进,两步向上行进,如果用数字“1”表示向右行走一格,数字“2”表示向上行走一格,如“11221”与“11212”就表示两种符合要求的不同走法,那么符合要求的不同走法的种数为( )
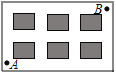
A. 6种B. 8种C. 10种D. 12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行,组委会为了做好运动员的保障工作,沿途设置了4个补给站,分别是:A(粤东农批)、B(奥体中心)、C(球王故里)和D(滨江中路),志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务,每个补给站被选择的可能性相同.
(1)小明选择补给站C(球王故里)的概率是多少?
(2)用树状图或列表的方法,求小明和小红恰好选择同一个补给站的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:如图1,昌平南环大桥是经典的悬索桥,当今大跨度桥梁大多采用此种结构.此种桥梁各结构的名称如图2所示,其建造原理是在两边高大的桥塔之间,悬挂着主索,再以相应的间隔,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,主索几何形态近似符合抛物线.

图1
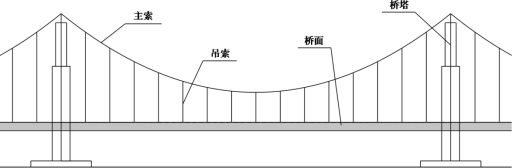
图2
材料2:如图3,某一同类型悬索桥,两桥塔AD=BC=10 m,间距AB为32 m,桥面AB水平,主索最低点为点P,点P距离桥面为2 m;

图3
为了进行研究,甲、乙、丙三位同学分别以不同方式建立了平面直角坐标系,如下图:
甲同学:以DC中点为原点,DC所在直线为x轴,建立平面直角坐标系;

乙同学:以AB中点为原点,AB所在直线为x轴,建立平面直角坐标系;

丙同学:以点P为原点,平行于AB的直线为x轴,建立平面直角坐标系.
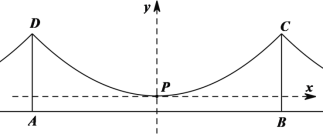
(1)请你选用其中一位同学建立的平面直角坐标系,写出此种情况下点C的坐标,并求出主索抛物线的表达式;
(2)距离点P水平距离为4 m和8 m处的吊索共四条需要更换,则四根吊索总长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A出发,沿边AB向终点B移动,同时点Q从点B出发,沿边BC向终点C移动.已知点P,Q的移动速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为xs.
(1)当x为何值时,四边形APQC的面积等于20![]() ?
?
(2)当x为何值时,△PBQ与△ABC相似?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com