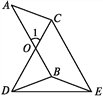
[题目]如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明理由. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明理由.

【答案】AC+BD=AB或AC+BD>AB，理由见解析

【解析】试题分析：根据平移的基本性质得出AB与CE平行且相等，再根据三角形的三边关系得出BE+BD=AC+BD＞DE=AB解答即可．

试题解析：由平移的性质知，AB与CE平行且相等，

所以四边形ACEB是平行四边形，BE=AC，

当B、D、E不共线时，

∵AB∥CE，∠DCE=∠AOC=60°，

∵AB=CE，AB=CD，

∴CE=CD，

∴△CED是等边三角形，

∴DE=AB，

根据三角形的三边关系知BE+BD=AC+BD＞DE=AB，

即AC+BD＞AB．

当D、B、E共线时，AC+BD=AB．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图,已知AB=10,点C,D在线段AB上,且AC=DB=2;点P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边三角形AEP和等边三角形PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,点G移动路径的长是_____.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某装修工程，甲、乙两人可以合作完成，若甲、乙两人合作4天后，再由乙独作12天可以完成，已知甲独作每天需要费用580元．乙独作每天需费用280元．但乙单独完成的天数是甲单独完成天数的2倍．
（1）甲、乙两人单独作这项工程各需多少天？
（2）如果工期要求不超过18天完成，应如何安排甲乙两人的工期使这项工程比较省钱？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（阅读理解）

“若满足，求的值”

解：设，则，

所以

（解决问题）

（1）若满足，求的值.

（2）若满足，求的值.

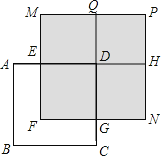
（3）如图，正方形的边长为，，长方形的面积是500，四边形和都是正方形，是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某工厂现有甲种原料3600kg，乙种原料2410kg，计划利用这两种原料生产A，B两种产品共500件，产品每月均能全部售出．已知生产一件A产品需要甲原料9kg和乙原料3kg；生产一件B种产品需甲种原料4kg和乙种原料8kg．

（1）设生产x件A种产品，写出x应满足的不等式组．

（2）问一共有几种符合要求的生产方案？并列举出来．

（3）若有两种销售定价方案，第一种定价方案可使A产品每件获得利润1.15万元，B产品每件获得利润1.25万元；第二种定价方案可使A和B产品每件都获得利润1.2万元；在上述生产方案中哪种定价方案盈利最多？（请用数据说明）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交于点F，交过点C的切线于点D．
（1）求证：DC=DP；
（2）若直径AB=12cm，∠CAB=30°， ①当E是半径OA中点时，切线长DC=cm：
②当AE=cm时，以A，O，C，F为顶点的四边形是菱形．