
分析 将A和C的坐标代入y1=k1x+b中,得到关于k1与b的方程组,求出方程组的解得到k1与b的值,确定出一次函数y1的表达式,将A的坐标代入反比例函数解析式,求出k2的值,得到反比例解析式,将一次函数解析式与反比例解析式联立即可求出B的坐标.
解答 解:∵将A(2,1),C(0,3)代入y1=k1x+b中,
得:$\left\{\begin{array}{l}{1={2k}_{1}+b}\\{3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=3}\end{array}\right.$,
∴y1的解析式为y1=-x+3,
将A(2,1)代入y2=$\frac{{k}_{2}}{2}$,
得:1=$\frac{{k}_{2}}{2}$,
解得:k2=2,
∴y2的解析式为y2=$\frac{2}{x}$,
∵解方程组$\left\{\begin{array}{l}{y=-x+3}\\{y=\frac{2}{x}}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
∴点B的坐标为(1,2).
点评 此题考查了反比例函数与一次函数的交点问题,以及利用待定系数法求函数解析式,灵活运用待定系数法是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
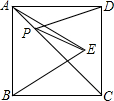 如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
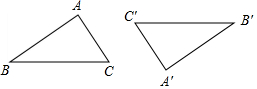 如图,在△ABC与△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需要增加一个条件,下列条件中不符合的是( )
如图,在△ABC与△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需要增加一个条件,下列条件中不符合的是( )| A. | ∠B=∠B′ | B. | ∠C=∠C′ | C. | AC=A′C′ | D. | CB=C′B′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727)
如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
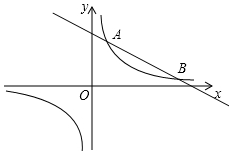 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com