
����Ŀ����֪������C1��y=ax2+bx+![]() ��a��0��������A��-1��0����B��3��0����
��a��0��������A��-1��0����B��3��0����

��1����������C1�Ľ���ʽ����д���䶥��C�����ꣻ
��2����ͼ1����������C1����ֱ��AC����ƽ�Ƶ�ij��ʱ�õ�������C2����ʱ��A��C�ֱ�ƽ�Ƶ���D��E�������F��������C1������x����·�������DEF����EFΪ�ĵ���ֱ�������Σ����F�����ꣻ
��3����ͼ2���ڣ�2���������£����M���߶�BC��һ���㣬EN��EM��ֱ��BF�ڵ�N����PΪ�߶�MN���е㣬����M�ӵ�B���C�˶�ʱ��
��tan��ENM��ֵ��α仯����˵�����ɣ�
����M�����Cʱ��ֱ��д����P������·�߳���
���𰸡���1��![]() ������C��1��2������2��F����3����6������3����tan��ENM=2���Ƕ�ֵ���������仯����
������C��1��2������2��F����3����6������3����tan��ENM=2���Ƕ�ֵ���������仯����![]() ��
��
�������������������1�����ݴ���ϵ����������ý���ʽ���ѽ���ʽ���ɶ���ʽ������ö������ꣻ
��2������A��C���������ֱ��AC�Ľ���ʽΪy=x+1�������������EF=4�����EF��y�ᣬ��F��m��-![]() m2+m+
m2+m+![]() ������E��m��m+1�����Ӷ��ó���m+1��-��-
������E��m��m+1�����Ӷ��ó���m+1��-��-![]() m2+m+
m2+m+![]() ��=4���ⷽ�̼������F�����ꣻ
��=4���ⷽ�̼������F�����ꣻ
��3����������ı���DFBC�Ǿ��Σ���EG��AC����BF��G��Ȼ�������EGN�ס�EMC����Ӧ�߳ɱ����������tan��ENM=![]() =2��
=2��
�����ݹ��ɶ������������������EN=![]() ��Ȼ�������������λ�߶���������ã�
��Ȼ�������������λ�߶���������ã�
�����������1����������C1��y=ax2+bx+![]() ��a��0��������A��-1��0����B��3��0����
��a��0��������A��-1��0����B��3��0����
��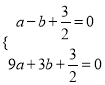 ���
���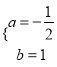 ��
��
��������C1�Ľ���ʽΪy=-![]() x2+x+
x2+x+![]() ��
��
��y=-![]() x2+x+
x2+x+![]() =-
=-![]() ��x-1��2+2��
��x-1��2+2��
������C��������1��2����
��2����ͼ1����CH��x����H��
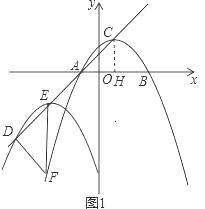
��A��-1��0����C��1��2����
��AH=CH=2��
���CAB=��ACH=45����
��ֱ��AC�Ľ���ʽΪy=x+1��
�ߡ�DEF����EFΪ�ĵ���ֱ�������Σ�
���DEF=45����
���DEF=��ACH��
��EF��y�ᣬ
��DE=AC=2![]() ��
��
��EF=4��
��F��m��-![]() m2+m+
m2+m+![]() ������E��m��m+1����
������E��m��m+1����
����m+1��-��-![]() m2+m+
m2+m+![]() ��=4��
��=4��
���m=3���ᣩ��m=-3��
��F��-3��-6����
��3����tan��ENM��ֵΪ��ֵ���������仯��
��ͼ2��
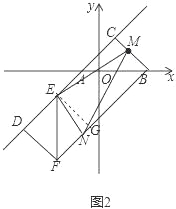
��DF��AC��BC��AC��
��DF��BC��
��DF=BC=AC��
���ı���DFBC�Ǿ��Σ�
��EG��AC����BF��G��
��EG=BC=AC=2![]() ��
��
��EN��EM��
���MEN=90����
�ߡ�CEG=90����
���CEM=��NEG��
���ENG�ס�EMC��
��![]() ��
��
��F��-3��-6����EF=4��
��E��-3��-2����
��C��1��2����
��EC=![]() =4
=4![]() ��
��
��![]() =2��
=2��
��tan��ENM=![]() =2��
=2��
��tan��ENM��ֵΪ��ֵ���������仯��
����P������·�����߶�P1P2����ͼ3��
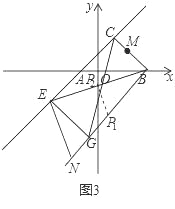
���ı���BCEG�Ǿ��Σ�GP2=CP2��
��EP2=BP2��
�ߡ�EGN�ס�ECB��
��![]() ��
��
��EC=4![]() ��EG=BC=2
��EG=BC=2![]() ��
��
��EB=2![]() ��
��
��![]() ��
��
��EN=![]() ��
��
��P1P2����BEN����λ�ߣ�
��P1P2=![]() EN=
EN=![]() ��
��
����M�����Cʱ����P������·�߳�Ϊ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���P��CD���е㣬��BCD=60�㣬����AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣬��BM��AE�ڵ�M����KN��AE�ڵ�N������MO��NO�������ĸ����ۣ��١�OMN�ǵ��������Σ���tan��OMN=![]() ����BP=4PK����PMPA=3PD2��������ȷ���ǣ�������
����BP=4PK����PMPA=3PD2��������ȷ���ǣ�������
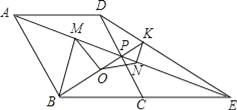
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����Ե������1������ƽ��ÿ�궼����5��������д������ĸ߶�y��cm����ʱ��x������֮��ĺ�����ϵʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ��ڹ涨ʱ��������24 000�����.��ÿ���ԭ�ƻ�������30�����,���ڹ涨ʱ���ڿ��Զ�����300�����.
��1����ԭ�ƻ�ÿ����������������涨������;
��2��Ϊ����ǰ�����������,�����ڰ���ԭ�й��˰�ԭ�ƻ�����������ͬʱ,����5�������������ˮ�߹�ͬ�����������,��֪ÿ�������������ˮ��ÿ����������ĸ�����20������ԭ�ƻ�ÿ�������������������20%.���˲���,ǡ����ǰ�������24 000���������������,��ԭ�ƻ����ŵĹ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=m��ƽ����X���ֱ�ߣ���������y=��![]() x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�BC���ϵĸ�AD=6��E�Ǹ�AD�ϵ�һ�����㣬F�DZ�AB���е㣬�ڵ�E�˶��Ĺ����У�����EB+EF����Сֵ���������Сֵ��( )
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ǹ��ݾ��꼶ij��50��ͬѧһ�ܵĶ���������Ƶ�����ͳ��ͼ��������ڸð�50��ͬѧһ�ܶ���ʱ���˵���������ǣ� ��

A. ��λ����6.5 B. ƽ������������
C. ����Ϊ3 D. ƽ��ÿ�ܶ�������6Сʱ����ռ������һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ����( )
A.a3��a2=a6
B.(a2)3=a6
C.(2a2)3=6a6
D.(-2a3)2=-4a6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com