练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．因式分解：
    （1）18axy-3ax2-27ay2
    （2）（a2+4）2-16a2
    （3）c（a-b）-2（a-b）2c+（a-b）3c．

    分析 （1）首先提取公因式-3a，进而利用完全平方公式分解因式得出答案；
    （2）直接利用平方差公式分解因式，进而利用完全平方公式分解因式得出答案；
    （3）首先提取公因式c（a-b），进而利用平方差公式分解因式得出答案．

    解答 解：（1）18axy-3ax2-27ay2
    =-3a（-6xy+x2+9y2）
    =-3a（x-3y）2；
    （2）（a2+4）2-16a2
    =（a2+4+4a）（a2+4-4a）
    =（a-2）2（a+2）2；

    （3）c（a-b）-2（a-b）2c+（a-b）3c
    =c（a-b）[1-2（a-b）+（a-b）2]
    =c（a-b） （a-b-1）2．

    点评 此题主要考查了提取公因式法以及公式法分解因式，正确应用公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．（1）若一抛物线的顶点在原点，且经过点A（-2，8），求抛物线的解析式；
    （2）如图，抛物线y=ax2+bx的顶点为A（-3，-3），且经过P（t，0）（t≠0），求该抛物线的解析式；
    （3）在（2）的条件下，回答下列问题（直接写出答案）
     ①y的最小值为-3；
     ②点P的坐标为（-6，0）；
     ③当x＞-3时，y随x的增大而增大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．若（x2+nx+3）（x2-3x+m）展开式中不含x2和x3项，求（n-m）n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

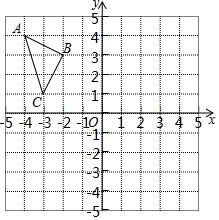    14．在如图的方格纸中，每个小正方形的边长都为l，△ABC的顶点坐标分别为A（-4，4）、B（-2，3）、C（-3，1）．
    （1）在图中画出与△ABC关于y轴对称的△A1B1C1，并直接写出△A1B1C1的三个顶点坐标；
    （2）画出将△A1B1C1向下平移4格得到的△A2B2C2，并直接写出△A2B2C2的三个顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．表是二次函数y=ax2+bx+c的部分x，y的对应值：
    x…-1-$\frac{1}{2}$0$\frac{1}{2}$1$\frac{3}{2}$2$\frac{5}{2}$3…
    y…m$\frac{1}{4}$-1$-\frac{7}{4}$-2$-\frac{7}{4}$-1$\frac{1}{4}$2…
    （1）二次函数图象的开口向上，顶点坐标是（1，-2），m的值为2；
    （2）当x＞0时，y的取值范围是y≥-2；
    （3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是n＞-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）（$\frac{7}{9}$+$\frac{5}{6}$-$\frac{3}{4}$-$\frac{11}{12}$+$\frac{7}{18}$）÷$\frac{1}{36}$
    （2）-8×（-2）4-（-$\frac{1}{2}$）3×（-16）+（-3）2×$\frac{4}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

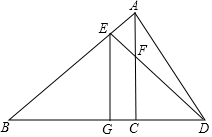    18．如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是AB上的一点，且在BD的垂直平分线EG上，DE交AC于点F，求证：点E在AF的垂直平分线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知一个多项式与单项式-7x5y4的积是21x5y7-28x7y4+14x6y4，求这个多项式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．小明说代数式$\frac{{x}^{2}-4}{x+2}$通过分子因式分解，变形为$\frac{（x+2）（x-2）}{x+2}$，然后分子分母约分化简为x-2，所以$\frac{{x}^{2}-4}{x+2}$和x-2是两个相同的代数式，因此$\frac{{x}^{2}-4}{x+2}$是整式，你认为他说的对吗？

    查看答案和解析>>

    同步练习册答案