
分析 (1)先将除法转化为乘法,再根据乘法分配律可以解答本题;
(2)根据幂的乘方、有理数的乘法、加法和减法可以解答本题.
解答 解:(1)($\frac{7}{9}$+$\frac{5}{6}$-$\frac{3}{4}$-$\frac{11}{12}$+$\frac{7}{18}$)÷$\frac{1}{36}$
=($\frac{7}{9}$+$\frac{5}{6}$-$\frac{3}{4}$-$\frac{11}{12}$+$\frac{7}{18}$)×36
=$\frac{7}{9}×36+\frac{5}{6}×36-\frac{3}{4}×36-\frac{11}{12}×36+\frac{7}{18}×36$
=28+30-27-33+14
=12;
(2)-8×(-2)4-(-$\frac{1}{2}$)3×(-16)+(-3)2×$\frac{4}{9}$
=-8×16-$(-\frac{1}{8})×(-16)+9×\frac{4}{9}$
=-128-2+4
=-126.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
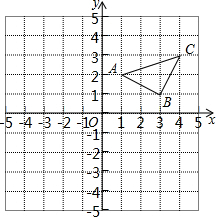 已知:如图所示,
已知:如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com