
 如图,点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上.
如图,点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上.分析 (1)直接利用反比例函数图象上点的坐标性质代入求出即可;
(2)根据平行四边形的性质得出D点纵坐标,进而代入函数解析式得出D点横坐标即可.
解答 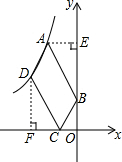 解:(1)∵点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上,
解:(1)∵点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上,
∴k=(1-$\sqrt{5}$)(1+$\sqrt{5}$)=1-5=-4;
(2)过点A作AE⊥y轴于点E,过点D作DF⊥x轴于点F,
∵四边形ABCD是以AB,AD为邻边的平行四边形ABCD,
∴DC$\stackrel{∥}{=}$AB,
∵A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),
∴BE=$\sqrt{5}$,
由题意可得:∠ABE+∠ABC+∠CBO+∠OCB+∠DCB+∠DCF=180°+180°=360°,
∵∠DCB+∠ABC=180°,
∴∠ABE+∠CBO+∠OCB+∠DCF=180°,
∵∠BCO+∠CBO=90°,
∴∠DCF+∠ABE=90°,
∵∠ABE+∠BAE=90°,
∴∠EAB=∠DCF,
在△BEA和△DFC中
$\left\{\begin{array}{l}{∠BEA=∠DFC}\\{∠EAB=∠FCD}\\{AB=DC}\end{array}\right.$
∴△BEA≌△DFC(AAS),
则DF=BE=$\sqrt{5}$,
则$\sqrt{5}$=$\frac{-4}{x}$,
解得:x=$\frac{-4\sqrt{5}}{5}$,
∴点D的坐标为:(-$\frac{4\sqrt{5}}{5}$,$\sqrt{5}$).
点评 此题主要考查了反比例函数综合以及平行四边形的性质,得出D点纵坐标是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=2,则线段ON的长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=2,则线段ON的长为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=16.
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读与计算:请阅读以下材料,并完成相应的任务.
阅读与计算:请阅读以下材料,并完成相应的任务.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
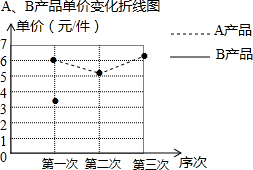 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如表统计表及不完整的折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如表统计表及不完整的折线图.| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com