
 如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.分析 (1)认真审题,直接根据题意列出方程组,求出B,C两点的坐标,进而可求出抛物线的解析式;
(2)分0<t<6时和6<t≤8时两种情况进行讨论,据此即可求出三角形的最大值;
(3)以点D为分界点,分2<t≤8时和t>8时两种情况进行讨论,再根据三角形相似的条件,即可得解.
解答  解:(1)由题意知x1、x2是方程mx2-8mx+4m+2=0的两根,
解:(1)由题意知x1、x2是方程mx2-8mx+4m+2=0的两根,
∴x1+x2=8,
由$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=8}\\{{x}_{2}-{x}_{1=}4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{x}_{2}=6}\end{array}\right.$
∴B(2,0)、C(6,0)
则4m-16m+4m+2=0,
解得:m=$\frac{1}{4}$,
∴该抛物线解析式为:y=$\frac{1}{4}{x}^{2}-2x+3$;
(2)可求得A(0,3)
设直线AC的解析式为:y=kx+b,
∵$\left\{\begin{array}{l}{b=3}\\{6k+b=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$
∴直线AC的解析式为:y=-$\frac{1}{2}$x+3,
要构成△APC,显然t≠6,分两种情况讨论:
①当0<t<6时,设直线l与AC交点为F,则:F(t,-$\frac{1}{2}t+3$),
∵P(t,$\frac{1}{4}{t}^{2}-2t+3$),∴PF=$-\frac{1}{4}{t}^{2}+\frac{3}{2}t$,
∴S△APC=S△APF+S△CPF
=$\frac{1}{2}(-\frac{1}{4}{t}^{2}+\frac{3}{2}t)•t+\frac{1}{2}(-\frac{1}{4}{t}^{2}+\frac{3}{2}t)•(6-t)$
=$\frac{1}{2}(-\frac{1}{4}{t}^{2}+\frac{3}{2}t)•6$
=$-\frac{3}{4}(t-3)^{2}+\frac{27}{4}$,
此时最大值为:$\frac{27}{4}$,
②当6<t≤8时,设直线l与AC交点为M,则:M(t,-$\frac{1}{2}t+3$),
∵P(t,$\frac{1}{4}{t}^{2}-2t+3$),∴PM=$\frac{1}{4}{t}^{2}-\frac{3}{2}t$,
∴S△APC=S△APM-S△CPM=$\frac{1}{2}(\frac{1}{4}{t}^{2}-\frac{3}{2}t)t-\frac{1}{2}(\frac{1}{4}{t}^{2}-\frac{3}{2}t)(t-6)$
=$\frac{3}{4}{t}^{2}-\frac{9}{2}t$
=$\frac{3}{4}(t-3)^{2}-\frac{27}{4}$,
当t=8时,取最大值,最大值为:12,
综上可知,当0<t≤8时,△APC面积的最大值为12;
(3)方法一:
如图,连接AB,则△AOB中,∠AOB=90°,AO=3,BO=2,
Q(t,3),P(t,$\frac{1}{4}{t}^{2}-2t+3$),
①当2<t<8时,AQ=t,PQ=$-\frac{1}{4}{t}^{2}+2t$,
若:△AOB∽△AQP,则:$\frac{AO}{AQ}=\frac{BO}{PQ}$,
即:$\frac{3}{t}=\frac{2}{-\frac{1}{4}{t}^{2}+2t}$,
∴t=0(舍),或t=$\frac{16}{3}$,
若△AOB∽△PQA,则:$\frac{AO}{PQ}=\frac{OB}{AQ}$,
即:$\frac{3}{-{\frac{1}{4}t}^{2}+2t}=\frac{2}{t}$,
∴t=0(舍)或t=2(舍),
②当t>8时,AQ′=t,PQ′=$\frac{1}{4}{t}^{2}-2t$,
若:△AOB∽△AQP,则:$\frac{AO}{AQ′}=\frac{BO}{P′Q′}$,
即:$\frac{3}{t}=\frac{2}{\frac{1}{4}{t}^{2}-2t}$,
∴t=0(舍),或t=$\frac{32}{3}$,
若△AOB∽△PQA,则:$\frac{AO}{P′Q′}=\frac{BO}{AQ′}$,
即:$\frac{2}{t}=\frac{3}{\frac{1}{4}{t}^{2}-2t}$,
∴t=0(舍)或t=14,
∴t=$\frac{16}{3}$或t=$\frac{32}{3}$或t=14.
方法二:
若以A、P、Q为顶点的三角形与△AOB相似,
则$\frac{PQ}{AQ}=\frac{AO}{BO}$或$\frac{PQ}{AQ}=\frac{BO}{AO}$,
设P(t,$\frac{1}{4}{t}^{2}-2t+3$)(t>2)
∴Q(t,3)
①|$\frac{\frac{1}{4}{t}^{2}-2t}{t}$|=$\frac{3}{2}$,∴|$\frac{t-8}{4}$|=$\frac{3}{2}$,∴t1=2(舍),t2=14,
②|$\frac{\frac{1}{4}{t}^{2}-2t}{t}$|=$\frac{2}{3}$,∴|$\frac{t-8}{4}$|=$\frac{2}{3}$,∴t1=$\frac{16}{3}$,t2=$\frac{32}{3}$,
综上所述:存在:t1=$\frac{16}{3}$,t2=$\frac{32}{3}$,t3=14.
点评 本题主要考查了抛物线解析式的求法,以及利用配方法等知识点求最值的问题,还考查了三角形相似的问题,是一道二次函数与几何问题结合紧密的题目,要注意认真总结.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 153.7×108 | B. | 15.37×108 | C. | 1.537×1010 | D. | 1.537×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
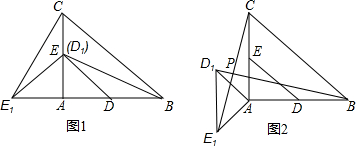
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上.
如图,点A(1-$\sqrt{5}$,1+$\sqrt{5}$)在双曲线y=$\frac{k}{x}$(x<0)上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com